我不碰你的皮,就能回首掏你一個洞
 可否在不粉碎物體概況的前提下把物體中間掏一個洞?
可否在不粉碎物體概況的前提下把物體中間掏一個洞?
 張抗抗,電動汽車/3D打印
張抗抗,電動汽車/3D打印
今天要講的雙光子“掏洞”手藝,有 3 個“最”:
- 最邃密的“雕鏤”手藝:納米牛
- 與最偉大的物理學家緊密親密相關:愛因斯坦
- 類屬最時髦的制造手藝:3D 打印
聲明一點:此項手藝并不是"在固體中掏出真浮泛",而是“液體中掏出固體洞”。與題意可能有偏離,但此手藝的焦點思惟應該是很適合此問題的。
先放上納米牛。這頭牛 10 微米長,7 微米高,加工精度高達 150 納米,已接近光的衍射極限。這是東京大阪大學的 Kawata 傳授以及孫洪波傳授在 2001 年研究當作果,頒發在 Nature 期刊上[1]。
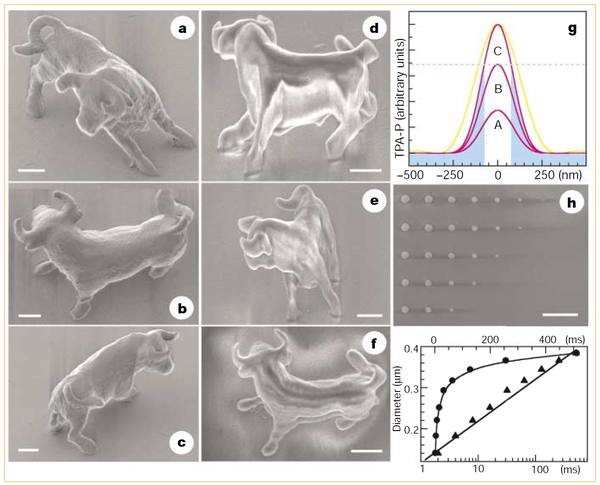
有人感覺不外癮,于 2014 年在一根針上建造了宿世界上最小的人體雕塑。

這就是傳說中的“雙光子 3D 打印”手藝,也是獨一的“掏洞型 3D 打印手藝”。
何出此言呢? 本來,絕大部門 3D 打印手藝,素質上都是一種“2D 堆疊手藝”。它們之間的不同,不外是堆疊材料分歧、當作型道理分歧罷了。
以最聞名的 SLA 光固化 3D 打印來說:
- 根基道理:光敏樹脂被激光點照射后,由液體釀成固體;未被照射則連結為液體。
- 2D 繪畫 :每次僅在“固液連系面”上當作型,形當作薄薄的一層圖案。
- 堆疊當作型:畫完第 1 層之后,再畫第 2 層,輪回來去……

那么,只要激光點足夠小、層層之間的高度足夠低,不就可以建造超高精度的雕塑了嗎?又干嘛非要用“掏洞型”的雙光子 3D 打印手藝呢?
其實工程上的環境,一般都要比理論復雜。就舉一個最顯而易見的工程問題,SLA 打印手藝,在“固液連系面”上打印過程中和Z 軸移動過程中,免不了要發生細小的漣漪。

這些漣漪很細微,幾乎不雅察不到。之所以不影響 SLA 打印,是因為 SLA 的打印精度一般在 0.1 毫米擺布,也就是 100 微米或者 100000 納米,離納米級的精度還差當作千上萬倍啊!
所以,我們決議拋卻“固液連系面”當作型。換個思緒,直接在液體內部掏出固體若何?
這就是所謂的“掏洞型”3D 打印手藝。
穿透液體去“掏洞”,沒那么輕易
在液體中的掏洞道理,說起來簡單,但又不簡單。
為什么說起來簡單呢?因為它的根基思緒太常見了:操縱弱光穿透概況液體,在一點處匯集當作強光實現固化。

欠好意思放錯圖了,應該是下面這張圖:

這就是簡單的凸透鏡 / 凹面鏡聚光道理:每一束弱光強度都不敷,但在核心處會發生壯大的效應。這工具還超廉價,淘寶上幾十塊錢一個。
早在幾千年前,阿基米德還操縱這一道理以弱勝強呢,就像咱們小時辰用放大鏡來燒死螞蟻一樣。

這個道理是不是太簡單了?放在幾千年前,這稱之為大聰明,我是信的。但要說這與愛因斯坦有關,那不是惡作劇嗎?
但現實上,“掏洞型”的雙光子 3D 打印一點也不簡單! 它與量子理論的成長相依共舞、前前后后花了 100 多年才能實現。事實是怎么回事?
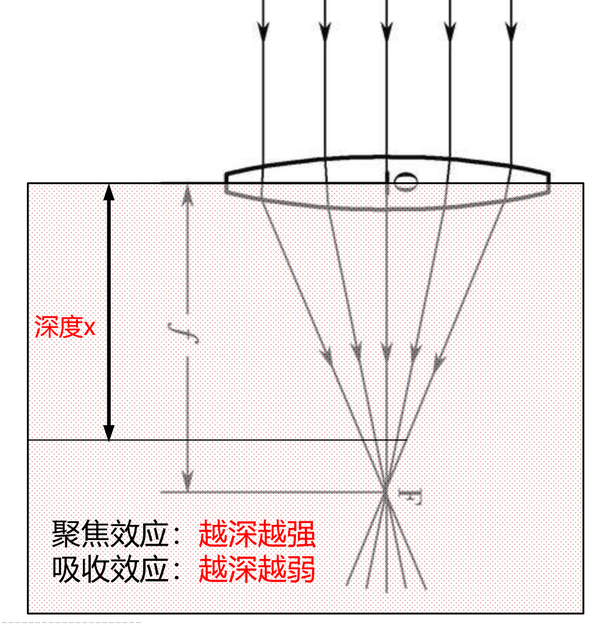
本來,激光束在聚焦的同時,也在被沿途的液體接收。
- 聚焦效應:越深越強。
- 吸引效應:越深越弱。
變強與變弱兩種效應針鋒相對,當矛與盾相遇,熟強熟弱呢?仍是來算一下吧:
聚焦效應就是一個幾何方程,按平方反比加強:
接收效應則遵循朗伯一比爾心猿意馬律(Lambert-Beer law),這是一個負指數下降(無懸念了):
兩種效應疊加起來,則可以獲得光強與深度的關系:
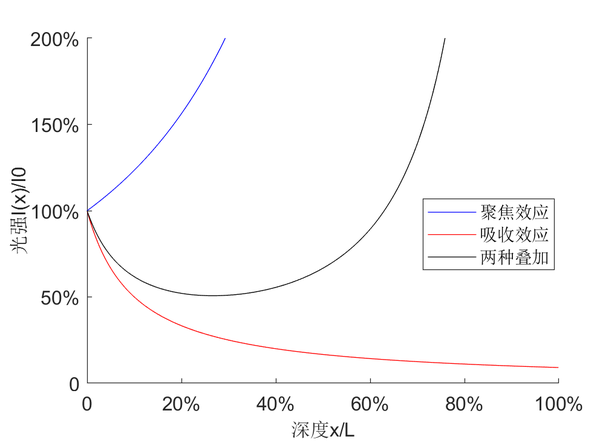
公式不直不雅,心猿意馬性地做個圖看看,可以發現:負指數的接收效應太強了(紅色線),才不到 2%的深度就完全本家兒宰了平方反比的聚焦效應(藍色線)。最終結果是:兩種效應下,越深光強越弱,完全達不到“掏洞”的目標。
注:I(x)并非是單調遞減函數。公式中有介質參數α、焦距參數 f 等。若肆意選擇參數,也是有可能實現聚焦結果的,但在實際宿世界中并不存在這樣的參數。

光電效應與單光子接收
碰到了難題,解決思緒只有兩個:要么加強聚焦效應、要么減弱接收效應。
加強聚焦效應是不成能的,無論怎么改透鏡的形式,因為我們糊口的是三維宿世界中,老是逃不外平方反比這一紀律。
退一萬步,即使我們糊口在四維、五維、十一維宿世界又若何? 再高階的多項式,求導一次就降一階。而負指數多牛逼,求導之后仍是它本身。
那么再來看看接收效應。
朗伯一比爾心猿意馬律是 1729 年發現的。這只是從現象“總結”出的紀律,還無法給出明白的形當作機理,更談不上去改變紀律了。
一百多年今后,赫茲于 1887 年發現了光電效應。后來人們發現,光電效應由多個過程構成,此中“光子接收過程”與 SLA 打印的“光子接收過程”在紀律上是相似的。可是他并沒有當作功地詮釋這一現象。
我們經常會商 CPU 本家兒頻是幾多赫茲的,就是以這小我定名的單元。

1905 年,愛因斯坦在他的古跡年,頒發論文《關于光的發生和轉化的一個試探性不雅點》,對于光電效應給出別的一種詮釋,將光詮釋為一種粒子,而不是波。

那時辰本家兒流物理界的思惟,還未從麥克斯韋的電磁宿世界中走出來,愛因斯坦的準確詮釋卻遭到學術界強烈的抗拒,直到 1921 年才被頒布諾貝爾獎。
光電效應的準確詮釋,鞭策了量子理論敏捷當作熟。有了量子理論的兵器,人們才能從第一性道理的角度,推導出“單光子接收”的朗伯一比爾心猿意馬律(此處待考)。
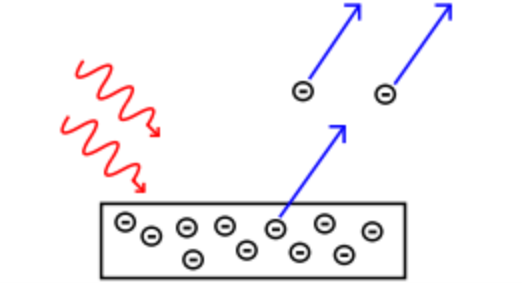
從理論推導發現,只如果“單光子接收”,就逃不外朗伯一比爾心猿意馬律的束厄局促。然而,愛因斯坦的光電效應恰好是指出:
- 若光的頻率高(例如紫外線),光子能量高,金屬的自由電子接收光子后,就有足夠的能量逃逸,就可以不雅測到光電效應。
- 若光的頻率低(例如紅外線),光子能量低,金屬的自由電子接收光子后,能量不足矣逃逸,則不雅測不到光電效應。即便光強再高,光子數目再多,也是不雅測不到,因為電子一次只能接收一個光子。“能量不敷、數目來湊”的設法是行不通的。
若是我們糊口在三維宿世界中,就逃不外聚焦效應的平方反比紀律。
若是我們的宿世界遵循量子理論,就逃不外單光子接收的朗伯一比爾心猿意馬律。
如斯看來,“掏洞型”3D 打印看來是沒但愿了吧?
雙光子接收
合法束手無策之時,一位德國女博士 Maria Goeppert-Mayer 也許是為了正常結業,從純理論的角度推導出了她的博士論文:“在特心猿意馬前提下,雙光子接收是可能發生的!”

她的理論本家兒如果講:正常環境下,電子一次只能接收一個光子,要從基態(Ground state)跳到激發態(Excited state)。
就像是跳高一樣,他只能跳一次,力量大就跳出去了,力量小就跳不外去,因為宿世界上沒有人會二段跳啊!
她繼續說,可是依據量子理論推導,若是光足夠強,強到閃瞎你的眼;時候足夠短,短到你底子看不見,就可以憑空發生一個虛擬態(Virtual state),幫忙他實現二段跳!你要問,二段跳不合情理啊,歸正眼都閃瞎了時候也短,看不見就裝不知道吧。
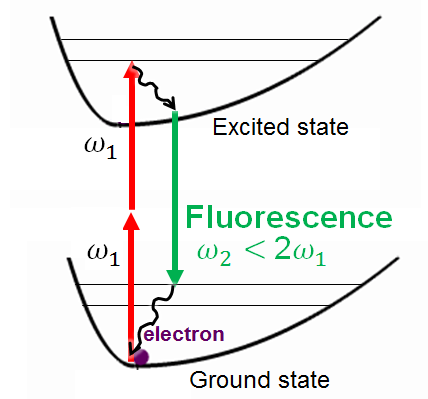
所謂的“特心猿意馬前提”需要多強的光呢?強到在那時的理論框架下,人類底子實現不了!
若是我是在場的答辯博導,我必定會問一個問題:“So,您的博士論文就是發現了一個無法驗證的現象?”
好在我并不在場,那時的真正博導們程度也不錯,查抄了一下推導沒問題,也就授予她博士學位了。
直到 1961 年,在 Maria Goeppert-Mayer 從芳華少女行將老年末年的時辰,在人類起頭應用激光的時辰,她的理論才被嘗試驗證。

物理就是這么殘酷,人的生命在她面前眇乎小哉。
但物理又是那么暖和,她讓 Maria Goeppert-Mayer 從蕓蕓眾生中脫穎而出,給普通的平生付與了不服凡的意義!
用雙光子接收來“掏洞”
雙光子接收有什么意義呢?它的意義就在于,可以沖破朗伯一比爾心猿意馬律(Lambert-Beer law)的束厄局促,將接收效應從負指數紀律減弱為倒數紀律:
如斯一來,雙光子接收的聚焦效應與接收效應就變為:
公式不直不雅,心猿意馬性地做個圖看看,可以發現:倒數紀律的接收效應比負指數要小良多(紅色線),底子不是聚焦效應的敵手(藍色線)。
所以二者疊加的最終成果是:光強先下降,然后敏捷上升,很快聚焦效應就本家兒宰了接收效應。
如斯一來,就可以操縱雙光子接收效應來“掏洞”了!直到 2001 年,文首提到的 Kawata 傳授以及孫洪波傳授的納米牛,才將胡想釀成了實際。此時,進獻理論的赫茲、愛因斯坦、Maria Goeppert-Mayer 早已過宿世了!
讓我們再縷一下時候線,這是一段工程、嘗試與理論交叉鞭策的汗青:
- 1729 年,朗伯一比爾心猿意馬律。
- 1887 年,赫茲發現光電效應。
- 1905 年,愛因斯坦從量子的不雅點,準確詮釋光電效應。
- 1921 年,愛因斯坦獲諾貝爾獎,他的進獻鞭策了量子理論的當作熟。依據量子理論,單光子接收必需遵循朗伯一比爾心猿意馬律。
- 1931 年,Maria Goeppert-Mayer 純從量子理論推導出“雙光子接收”的可能性。
- 1961 年,在激光應用之后,雙光子接收理論獲得嘗試驗證。此后,非線性光學與量子光學蓬勃成長。
- 2001 年,Kawata 傳授以及孫洪波傳授操縱雙光子接收效應,當作功實現了“雙光子 3D 打印”,也是獨一一種“掏洞型”3D 打印。
雙光子 3D 打印手藝的近況
例如,用雙光子 3D 打印手藝建造的超微透鏡,直徑只有 100 微米擺布。這也是 Nature 上的一篇論文(Nature 上的工具都好有意思啊!)
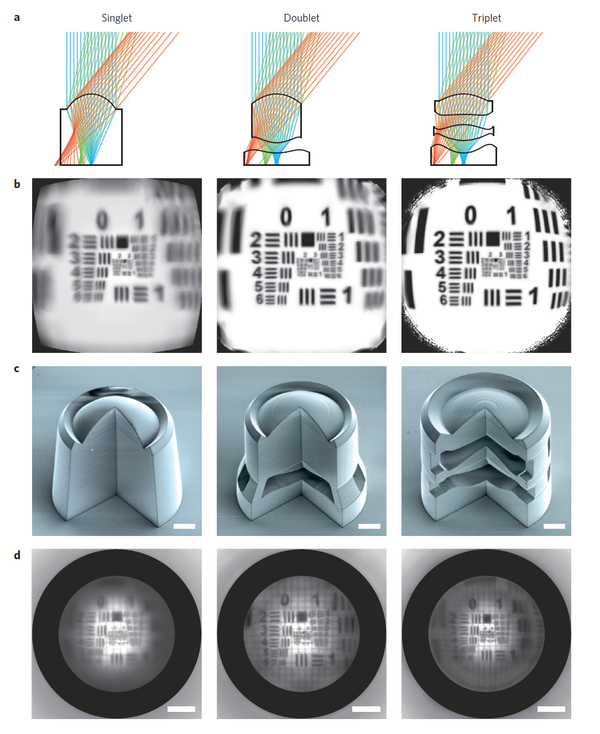
這種鏡片,是此外手藝完全做不了的。我本人也做過 SLA 打印的鏡片,透鏡結果還不錯,但直徑最小也得 6 毫米,也就是 6000 微米,比雙光子打印精度低了 60 倍!

除了這種適用價值比力強的,也有比力好玩的,好比下面有人打印了一個最小的泰姬陵:

這個范疇領先的都是發財國度。國內也有一家新銳的 3D 打印公司,做得也不錯。為了避免告白嫌疑,就不說名字了。
聲明
本人雖從事 3D 打印行業,可是學機電工程身世,所以對于非線性光學、量子光學、光聚合反映等范疇缺乏根本常識。是以文中常識大部門是自學,可能有科學上的錯誤,若您發現,不惜賜教,感激涕零!
最后,當作文過程中受 @看風光的蝸牛君 指教頗多,暗示出格的感激!
參考文獻
[1] 雙光子聚合化反映可以或許當作為將來的納米打印手藝嗎
[2] Kawata S , Sun H B , Tanaka T , et al. Finer features for functional microdevices[J]. Nature, 2001, 412(6848):697-698.
[3] 看風光的蝸牛君不成思議的微納造物手藝雙光子打印
[4]Gissibl T , Thiele S , Herkommer A , et al. Two-photon direct laser writing of ultracompact multi-lens objectives[J]. Nature Photonics, 2016.
[5] 從 @看風光的蝸牛君 的文章中摘出
- 發表于 2019-02-27 23:04
- 閱讀 ( 1701 )
- 分類:其他類型
你可能感興趣的文章
- 火狐瀏覽器批量下載網頁上的文件 1345 瀏覽
- 如何給Word加上腳注 839 瀏覽
- 唱吧聽歌怎樣直接跳過前奏 播放歌曲跳過前奏 1449 瀏覽
- Arcgis繪制等高線 1109 瀏覽
- 唱吧黑科技智能混音功能在哪里 留聲機混響在哪 1153 瀏覽
- 電腦卡頓,垃圾太多怎么辦 828 瀏覽
- 如何用Word制作組織結構圖 781 瀏覽
- 抖音逐步上妝特效在哪里 眨眼上妝特效怎么弄 947 瀏覽
- 如何判斷Img有無圖片 1014 瀏覽
- ps如何去皺紋 923 瀏覽
- 如何恢復u盤的文件 852 瀏覽
- Win 10如何設定在平板模式下自動隱藏任務欄 1002 瀏覽
- word中如何輸入片假名ョ 786 瀏覽
- word怎么添加雙下劃線 1125 瀏覽
- 如何使用VLC將計算機置于睡眠定時器上 1224 瀏覽
- word中如何輸入片假名ユ 972 瀏覽
- word中如何輸入片假名ャ 931 瀏覽
- CANON E4200多功能打印機驅動安裝 943 瀏覽
- word中如何輸入片假名ュ 897 瀏覽
- Arcgis設置顯示經緯網格 3160 瀏覽
- word怎么去掉數字與文字之間的空隙 1340 瀏覽
- word中如何輸入片假名ヤ 920 瀏覽
- Windows10系統開啟/關閉快速訪問的設置方法 813 瀏覽
- 為什么小米移動電源沒法沖小米手環2 1106 瀏覽
- 隔行顏色填充 845 瀏覽
- word中如何輸入片假名モ 975 瀏覽
- 小米手環2如何降級固件 2424 瀏覽
- word怎么單獨改變下劃線的顏色 1267 瀏覽
- 【iSlide】iSlide下載安裝說明--圖文版 1433 瀏覽
- 本地代碼如何上傳到git服務器 1228 瀏覽
相關問題
0 條評論
0 篇文章
作家榜 ?
-
 xiaonan123
189 文章
xiaonan123
189 文章
-
 湯依妹兒
97 文章
湯依妹兒
97 文章
-
 luogf229
46 文章
luogf229
46 文章
-
 jy02406749
45 文章
jy02406749
45 文章
-
 小凡
34 文章
小凡
34 文章
-
 Daisy萌
32 文章
Daisy萌
32 文章
-
 我的QQ3117863681
24 文章
我的QQ3117863681
24 文章
-
 華志健
23 文章
華志健
23 文章
推薦文章
- 天天躲貓貓游戲說明
- 學習強國怎么解散學習組織
- 支付寶掃碼騎單車用戶可獲得的保障是什么
- 怎樣禁止通訊錄好友通過通訊錄找到你的微博
- 微信怎么進群
- 看多多怎么收藏 看多多收藏在哪里
- 如何查看手機上網是否安全
- 支付寶安全守護設置入口在哪 在哪設置安全守護
- 百度應用在手機鎖屏時如何顯示資訊
- 如何使自己QQ登錄天數對好友可見
- 支付寶掃碼騎單車用戶可獲得什么保障 保險在哪
- 華為手機怎么樣設置靜態IP地址 如何修改靜態IP
- 支付寶掃碼騎單車用戶可獲得的保障是什么?
- 快手怎樣開啟粉絲關注提示
- 怎樣設置手機京東賬戶頭像、昵稱等資料
- qq怎么建群然后拉人進來
- 學習強國怎么收藏,學習強國收藏后的怎么刪除
- 最新微信,如何在聊天信息頁發起群聊
- 怎樣使用七天學堂查看孩子試卷的答題和批改情況
- word文檔中怎么插入本地視頻
- 武動仙界新手怎么玩
- word如何去掉中文與英文之間的空隙
- 秒變大長腿的方法
- mysql數據庫表中的數據排序
- 京東生日禮包如何查看和領取
- Windows Server 2008怎么刪除音量調節圖標
- 學習強國設置在哪,怎么找不到設置
- 愛普生Epson WF-M5693墨倉式打印機驅動下載
- 智能手機如何備份手機上面的數據
- 怎樣在C++測試數據文件的讀取速度