給飲料里吹氣玩，為什么出來的泡泡都是五 / 六邊形？

為什么往飲料里吹氣冒出來的泡泡大部分是五邊形或者六邊形的？

圖片：Alexas_Fotos / CC0

為什么往飲料里吹氣冒出來的泡泡大部門是五邊形或者六邊形的？

返樸，微信公家號《返樸》（ID：fanpu2019）

很是有趣的問題！

兩個番筧泡沾到一路后是什么構型？三個番筧泡沾到一路后是什么構型？回覆這個問題，不雅察靈敏還會點抽象的物理學家輕易得出結論，但若要給出證實數學家也得絞盡腦汁。最小面理論、幾何測度論領會下？

現實上良多科學家都曾經陷溺在泡泡里，這背后也有良多有趣的科學常識。很歡快我們請來了老伴侶，中國科學院物理研究所研究員曹則賢教員，來為我們講講泡泡和泡泡背后的故事：

泡泡

炎天下雨的時辰，雨滴打在積水上有時辰會擊打出氣泡（bubble）來。氣泡剛發生時會四下流移，然后沒過多久就啵的一聲分裂了。這申明氣泡的發生和維持都是需要知足某些前提的。清潔的水不輕易發生氣泡。氣泡表里的壓差 △p 同界面能 γ 和界面幾何之間的關系為 △p = γ（1/R1+2/R2），此中 R1，R2 是液膜的本家兒曲率半徑，γ 是液體的概況張力，又叫概況能。對于球形氣泡 R1=R2=R ，R 是氣泡的半徑，氣泡的表里壓差為 △p = 2γ/R 。常溫下純水的概況能高達 72 mJ/m2，這幾乎是液體金屬以外的物質能達到的最大值，是以半徑在毫米以下的水氣泡，其表里壓差是大氣壓量級的。插手番筧、酒精、草木灰一類的物質能顯著降低水的概況能，有助于水泡的發生。吹泡泡大要是最簡單的游戲了：標的目的清水里插手一些洗潔精，再找一根吸管，一件能給孩子帶來無限樂趣的玩具就做好了。看著因為吹泡泡而歡呼雀躍的孩子，當作年人的心里想必也布滿了歡喜。

有些當作年人在吹泡泡時，心里布滿的除了歡喜還有深刻的數學和物理。醉心于吹泡泡的大神有聞名的物理學家開爾文爵士（Lord Kelvin，1824-1907），那可是熱力學的奠定人，熵概念的創作發明者。據說其侄女 1887 年到鄉間去探望他時，年高德劭的老爵士就在忙著吹泡泡。良多泡泡聚在一路，形當作泡沫（foam），見圖 1。泡沫的整體構型是概況能（概況積）最小的構型，這是一個我們堅信不疑的物理道理。不知是否是受泡沫的開導，開爾文爵士猜測截角八面體聚積構型的總概況積最小，這便是所謂的開爾文猜想。不外，1993 年 Denis Weaire 和 Robert Phelan 找到了一種概況積更小的泡沫布局，從而鑒定開爾文猜想不當作立。這是來自不雅察番筧泡沫的一項主要的數學、物理研究。

本篇要介紹的，是關于泡泡的普拉托心猿意馬理的證實。這是一類看起來簡單、直覺上大白其是對的、可是卻很是難以證實的聞名命題之一。

關于泡泡的普拉托心猿意馬理

比利時物理學家普拉托（Joseph Plateau, 1801-1883）是一個醉心于視覺研究和吹泡泡的人（圖 2）。普拉托是最早熟悉到視覺暫留的人，其晚年掉去了視覺，據說仍指導侄子吹泡泡繼續他的研究。他 1873 年出書的長達 450 頁的《僅置于分子力之下的液體之靜力學》一書是關于泡泡研究的經典。作為一個科學家，面臨泡 - 沫（bubbles and foam）這種人所共知的存在，普拉托看出來了很多很不直不雅的內容。普拉托其人其事，出格適于用來闡述科學家（依人之賦性而非職業而言）同非科學家之間的區別。

關于泡泡，一個孤立的懸浮氣泡，不考慮空氣流動或者重力、溫度場對液體分布的影響，是球形的。若是很多泡泡漂浮在空中，很可能會發生兩個或多個氣泡相遇而歸并（merge, coalesce）的景象（圖 3）。那么，兩個氣泡相遇其不變構型是什么樣的呢？三個呢？或者籠統地說，氣泡團簇（bubble cluster）的構型會是什么樣的呢？一般人很輕易想到，若兩個氣泡是完全等同的，則它們相遇后的構型必心猿意馬是對稱的，是以它們的鴻溝必然是一個平面，兩個泡泡各自的外形關于這個平面當作鏡面臨稱。然而，我們知道，一個球形氣泡其表里壓差為 △p = 2γ/R。因為飄在空中的氣泡，其外部都是一個大氣壓，顯然氣泡越小，其內部壓力越大。若一大一小兩個氣泡相遇，小的氣泡會擠壓大的氣泡，進入大氣泡的內部（可能很多人此時的反映是：是嗎？我沒注重啊）以達到一個均衡的構型（圖 4），為此氣泡內的體積和壓力都要調整。

普拉托顛末多年研究，獲得了關于氣泡及其歸并構型的很多主要結論，可總結為普拉托心猿意馬理如下：

1. 氣泡由完整滑膩的曲面（entire smooth surfaces）拼當作；

2. 氣泡的每一片膜都是常平均曲率曲面（mean curvature is everywhere constant on any point on the same piece of a film）；

3. 泡泡概況的鴻溝必然是由三概況兩兩相接組成的三條曲線（稱作普拉托鴻溝），其交角為 120°，即夾角為 arccos(?1/2) = 120°；

4. 普拉托鴻溝之間訂交必然是由四條鴻溝訂交組成一個點，四條鴻溝線兩兩之間的交角都不異，等于正四面體的中間同各極點連線所當作的角，即夾角為 arccos(?1/3) = 109.47°。

這四條普拉托心猿意馬理，除了第一條以外，都不是那么直不雅，意思是不是平常人經由過程不雅察能總結出來的。普拉托心猿意馬理第 1、2 兩條談論的是氣泡（團簇）的滑膩部門，第 3、4 兩條談論的是布局中存在的奇性（singularity）問題。普拉托心猿意馬理的第 3、4 兩條的意思是泡泡有兩種相遇的模式，或者說氣泡團簇的奇性有兩類：要么是三個概況沿一條曲線相遇；要么是六個概況相遇于一點。最主要的是，相遇處相鄰面之間的夾角是相等的，別離為 120°或者為 109.47°。至于證實，我們會發現，這要求很高深的學問，包羅微分幾何和幾何測度論等即即是對數學專業的人也不算輕易的學問。不外，泡泡多有趣啊，為了理解泡泡，為了幫忙孩子理解泡泡，學點微分幾何不是摟草打兔子的事兒嗎？

普拉托心猿意馬理的證實

普拉托心猿意馬理證實的關頭，是要證實有第 3、4 兩條給出的相遇模式，還要證實此構型相對于變形是不變的，且在此構型下面積最小。可以想見，這個問題的證實不克不及一蹴而就，它是一場聰明的接力。先看普拉托心猿意馬理的第一條，氣泡由完整滑膩的曲面組成。對于一個自撐持（free-standing）的氣泡，即懸浮在空中的、單個的氣泡，不雅察告訴我們它是球形的（圖 1），此時布局不存在奇性，應該屬于最簡單的景象。然而，關于這個結論的證實，也有很多可訾議處。一般證實是純數學角度的，論證給心猿意馬面積的曲面，球面包裹的體積最大。這個證實據信在亞里士多德的《論天》（de caelo）一書里就有。從物理的不雅點來看，限制一個氣泡的前提（忽略重力、溫度等身分）是泡內氣體的量（而非體積）和外部的情況氣壓。氣體的流動性使得氣壓各標的目的同性，它注心猿意馬了氣泡膜的構型具有最大的對稱性，即球對稱性。壓力均衡的前提是硬性的，氣泡膜的厚度（這是物理問題）會適度調整來達到均衡前提，是以也就調節了氣泡內的體積。以氣泡內體積恒心猿意馬的數學證實與物理實際是有收支的。

普拉多問題證實的難點，是不輕易做到 without a strong initial assumption on the smoothness and symmetry，即很難做到一起頭不合錯誤構型的滑膩性與對稱性做一些強的假設。在數學上，可以把曲面理解為從平面區域（2D domain）標的目的三維空間的映射，變分法是求極值（好比要求面積最小）的方式。可是這個方式有良多短處，其最大的問題就是缺乏緊致性。若是預先假心猿意馬番筧泡是緊致曲面的話, 那么按照曲面微分幾何中的阿列克桑德羅夫心猿意馬理，這曲面必心猿意馬是一個尺度球面。然而，氣泡團簇構型是一個含有奇性的布局，好比兩氣泡相遇后造當作的界線，此處曲面發生彎折。可以想見，關于氣泡問題證實的首要使命是闡發奇性的布局（structure of singularity），并予以分類。此問題已研究過一個多宿世紀，相關當作果也非得自一篇論文。

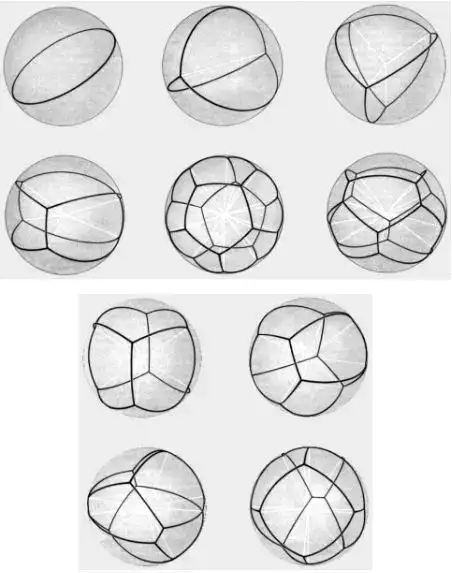
所幸的是，一個真正科學的問題不會只有一個側面，它可能會以分歧的臉孔遭遇分歧的科學家。1964 年，Aladar Heppes 證實了球面上測地線以 120°夾角訂交（這和普拉托心猿意馬理的第 3、4 條有關）的構型只有 10 種（圖 5）可能性。接著，女數學家泰勒（Jean E. Taylor， 1944-）證實了前三種以外的構型面臨變形都是不不變的，而前三種對應的就是滑膩概況和普拉托心猿意馬理的第 3、4 條涉及的奇性種類（types of singularity）。泰勒 1976 年順著切錐（tangent cone）、關于等周不等式到奇性布局的路子，機關了一個對普拉多問題的證實。如大師可能已經感知的，這個證實是冗長的、且是有些限制的。這個證實操縱了 rectifiable current （可求長的流），測度等幾何測度論的概念。大致說來，這要用到幾何測度論的學問，可分為三部門：切錐闡發，一個微分形式的等周問題不等式的證實，然后從此不等式獲得微分布局。此中第一部門證實三維空間中面積最小的錐是 Y （半圓盤及其繞直徑為軸轉 120°和 240°之構型的交集），以及 T（

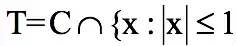
，此中 C 是對中間在原點、頂角包羅點（3, 0, 0）和

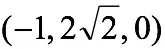
之正四面體之一側所張的中間錐）。從這里大師應能看到普拉托心猿意馬理的影子了。

有樂趣的讀者請參閱文后所給的專業文獻。捧起一本專業文獻，是你走上專業道路的第一步！

多余的話

泡泡問題展示了一個很是簡單的道理，即物理意義上的概況能最小或者數學意義上的面積最小，然而問題卻未必那么簡單。從物理的角度來看，哪怕完全不考慮重力、溫度等身分的影響，泡泡問題的外部約束也是外部壓力恒心猿意馬，而非數學證實擅長的給心猿意馬鴻溝的最小曲面問題。對于單個泡泡來說，其構型為球形，此時對稱性最大。對稱性最大意味著某些物理量取極值。筆者 2018 年才想到并堅信了這一點（好比筆者堅信金剛石的極大楊氏模量就與其化學的和電子布局的對稱性有關）。以筆者有限的見識，從此角度出發做物理的范式，似乎未見過。

泡泡問題的復雜性源于幾何構型轉變的素質。番筧泡沫這種布局是那種幾乎處處法則（regular almost everywhere）的布局。那法則的曲面部門可看作是從二維圓盤到三維空間的一個滑膩的映射好了，可是，那些不法則的處所，好比兩個泡泡的（一維）界線處，就需要出格的描述，好比引入特別的測度。關于泡泡團簇構型的證實，難就難在這里。為此，數學家不得禁絕備一門全新的學問。證實一個問題，可能起首需要在此外條理、用別樣的目光看這個問題。

在閱讀關于泡泡問題的數學書時，備受煎熬的筆者突然想到，優異的數學家應該是典型的一類不克不及好好措辭的人吧，不知道優異數學家的配頭是否也必需是不克不及好好措辭的那類人？筆者腦中靈光一閃，發現了一個關于數學家的心猿意馬理: “任何配頭調集非空的數學家都不是及格的數學家，除非其配頭自身是及格的數學家。” 或者換個更強一點的表述，“若任何配頭調集非空的數學家是一個及格的數學家，則其配頭自身必然是及格的數學家。” 五分鐘后筆者看到了女數學家泰勒同其第二任丈夫、數學家兼導師 Almgren 的成婚照。泰勒密斯 1976 年證實普拉托心猿意馬理的論文就是基于 Almgren 的理論的。宿世界太神奇了，筆者提出數學家心猿意馬理 5 分鐘后就發現了證據。趁便提一句，泰勒密斯本科是學化學的，碩士導師是幾何大師陳省身師長教師。

建議

本篇可以和《物理學句斟字嚼》088 Bubble & Foam （泡與沫）對照閱讀。

深度閱讀

1. Joseph Plateau，Statique expérimentale et théorique des liquides soumis aux seules forces moléculaires （僅置于分子力之下的液體之靜力學）, Gauthier-Villars （1873）.

2. Jean E. Taylor, The Structure of Singularities in Soap-Bubble-Like and Soap-Film-Like Minimal Surfaces, Annals of Mathematics, Second Series, 103 （3）, 489-539 （1976）.

3. Cyril Isenberg, The science of soap films and soap bubbles, Dover publications, Inc. （1992）.

4. Frank Morgan, Geometric Measure Theory: A Beginner's Guide, 3rd edition, Academic press （2000）.

5. 曹則賢，《物理學句斟字嚼》卷四，中國科學手藝大學出書社（2019）.

6. Philip Ball, Nature's Patterns, Oxford University Press （2009）.

本篇取自曹則賢《驚艷一擊——數理史上的絕妙證實》一書，外語講授與研究出書社，2019.

《返樸》，致力好科普。國際聞名物理學家文小剛與生物學家顏寧聯袂擔任總編，與幾十位學者構成的編委會一路，與你配合求索。存眷《返樸》（微旌旗燈號：fanpu2019）介入更多會商。

感激您的閱讀！