這個捆綁游戲，五百年來難住了無數高智商
給孩子最好的科學教育
在日本朝日放送的一檔叫做探偵!ナイトスクープ Knight Scoop 的節目里，有一個叫做秋原俊彥的 73 歲老爺爺在大夫的診室里看到了一個游戲，然后深深切迷。他求大夫把這個游戲送給他，然后在家花了 10 年時候想解開，可是做不到。不單秋原老爺子解不開，大大都不雅眾也被難住了。
這個游戲是這樣的——
這個游戲的方針是，在不暴力拆解的環境下，讓銀環從綠球這里到另一邊的紅球這里。
你想到的方式大師都想過了，都不是解法。
銀環不成能套過中心那個木頭環——
銀環也不成能從木頭環的中心穿曩昔——
基座拆不開，繩索也繞不外去——
現實上，難住老爺爺的這個解密游戲汗青悠長，也曾經難住了一代又一代的人。可是因為它的魅力龐大，所以一向傳播到此刻，并且傳布到了很多國度，在西方和東亞都有分歧的版本。
你能解開這個繩結綁縛游戲嗎？
關頭概念
所羅門封印
材料和操作
一根木條（也可以用粗一點的吸管取代）
一根繩索
兩個圓環
在木條上打 3 個洞，然后把繩索和圓環按照上面圖片里的樣子組裝好，就可以起頭玩啦。這個版本其實和一起頭介紹的那個游戲是一樣的事理，解法也是近似的。
這個游戲的方針是，讓右邊的那個圓環和左邊的圓環貼在一路。不克不及把木條弄斷，也不克不及把繩索剪斷。
你想到解答方式了嗎？
若是你感覺有點難，那先用下面這個簡單的標題問題來熱熱身吧。
看看下面這個環境，應該如何把插頭松綁？
其實這個插頭是這樣解出來的——
再來一道近似的題，求若何給本身松綁？
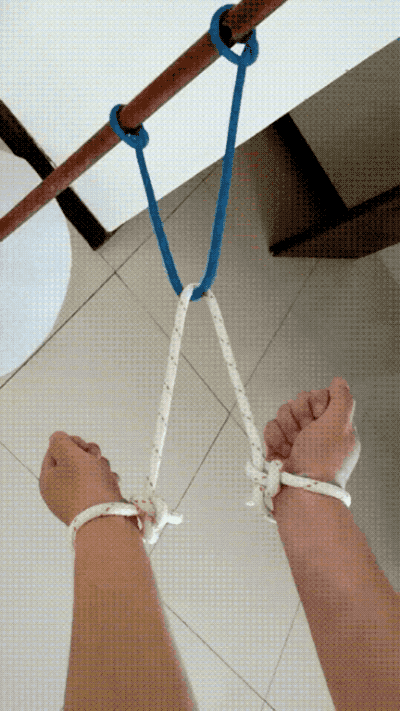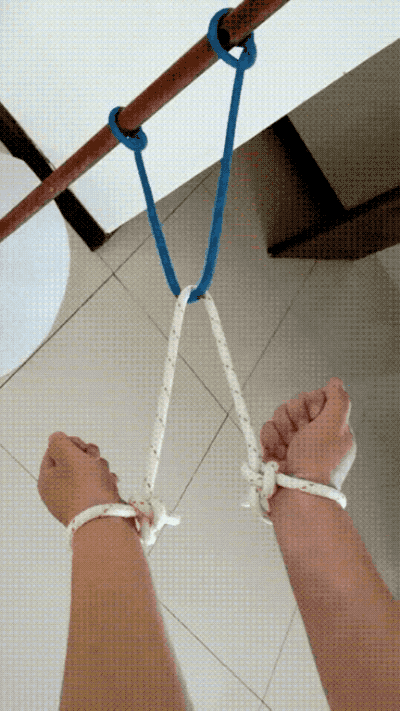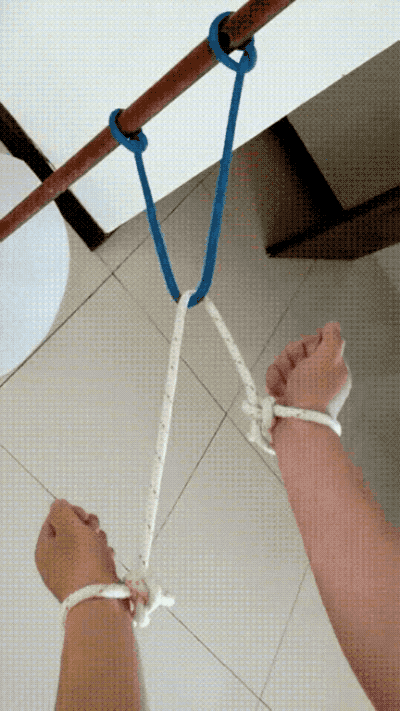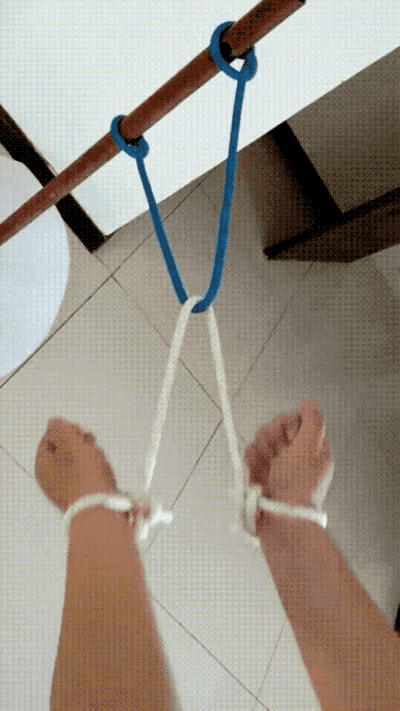
解法——
這有沒有給你一點啟迪呢？
若是你仍是不知道應該怎么解，在 把科學帶回家 后臺答復 求求你告訴我，就可以獲得謎底啦。
?
道理
在這檔 Knight Scoop 節目里，后來在日本知惠之輪協會的山本徹的幫忙下，這個謎題終于獲得領會答。
這個解密游戲，在西方有 wedding rings，the ox yoke，loop de loop，african ball 或者 Solomon’s seal 等各類名字。
這個游戲最早可以追溯到 16 宿世紀的意大利的數學家，達·芬奇（為什么老是你？）的老友盧卡·帕西奧利（Luca Pacioli）撰寫的《De Viribus Quantitatis》（數字的力量）。
這個游戲也有東亞的版本。這幅 1836 年的日本丹青里也描畫了這個游戲，這也是我們上面介紹手工建造的版本。
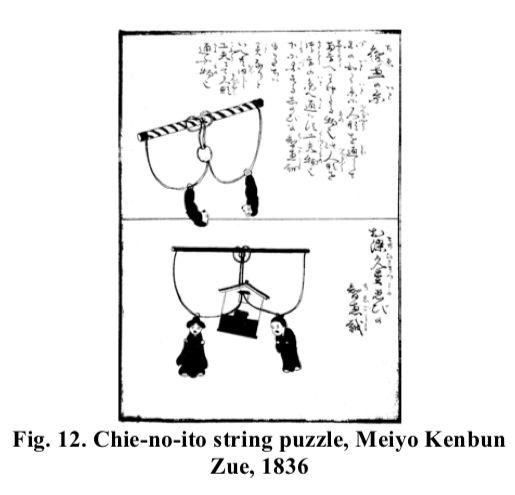
這個游戲的設心猿意馬是這樣的，情人 Osome 和 Hisamatsu 因為某些原因分手了，你要盡力使他們從頭在一路。
有良多適用本家兒義的人會說，這些游戲有什么用？
其實，這些游戲和拓撲學有關。汗青上拓撲學游戲曾經開導了主要的數學發現。
好比，柯尼斯堡七橋問題（Konigsberg bridge）問題就開導了歐拉。歐拉在 1736 年寫了一篇論文證實這個問題無解。歐拉的這篇論文當作為圖論這個數學分支的發源。
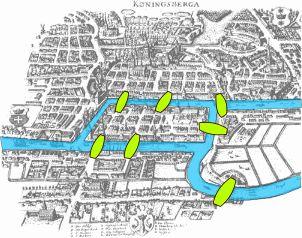
柯尼斯堡七橋問題：那時東普魯士柯尼斯堡（今日俄羅斯加里寧格勒）市區跨普列戈利亞河兩岸，河中間有兩個小島。小島與河的兩岸有七條橋毗連。在所有橋都只能走一遍的前提下，若何才能把這個處所所有的橋都走遍？
@wikipedia
?
若是上面這些游戲都難不倒你，可以試一試下面這個進階版本的拓撲游戲。你感覺在不暴力拆解的環境下，左圖可能釀成右圖嗎？
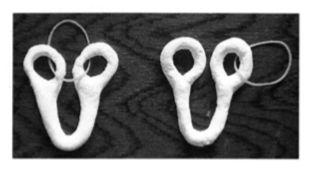
這個拓撲游戲其實想表達的是拓撲學里的一個根本概念：咖啡杯的拓撲形態和甜甜圈是一毛一樣的。
?
@wikipedia
?
好了，在拓撲學里的解法如下。
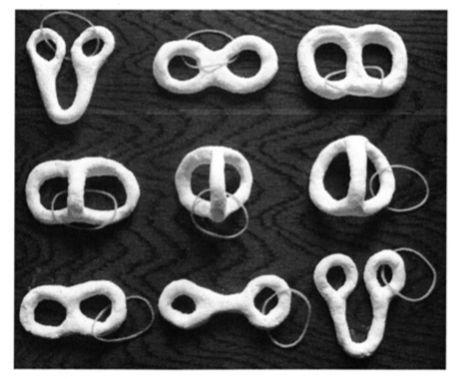
@西山豊，大阪經濟大學
?
好的我知道又有人要問：“這有什么用？”
良多人不是想知道小昭戴著枷鎖是怎么更衣服的嗎？
這就是金庸埋沒的拓撲學謎底啊！你把白色的工具算作手銬，把雙手合十的小昭算作是一個圈，你看在拓撲學的宿世界里小昭的鏈子底子就沒有同時銬住她的雙手啊。
(?? ?д?? )?
大要就是因為小昭暗自把握了這個拓撲學常識，所以金庸大俠才在《倚天屠龍記》跋文里提到小昭是他在書中最喜愛的腳色吧。
- 發表于 2019-07-25 23:36
- 閱讀 ( 972 )
- 分類：其他類型
0 篇文章
作家榜 ?
-
xiaonan123
189 文章
-
湯依妹兒
97 文章
-
luogf229
46 文章
-
jy02406749
45 文章
-
小凡
34 文章
-
Daisy萌
32 文章
-
我的QQ3117863681
24 文章
-
華志健
23 文章