有哪些有趣的概率問題？

圖片：TymonOziemblewski / CCO

張翼騰，復旦大學數學系

風險投資陷阱：做的每一筆投資都是正收益的，可是最后幾乎會變得一無所有。

在進行投資或者采辦股票的時辰，預期收益是一個很是主要的參考。當今越來越多的人接管概率的不雅點，知道固然買彩票或者賭錢有可能暴富，可是因為從期望角度而言每買一張彩票或者是下一個賭注都是吃虧的，所以從理性角度不該該進行這一筆買賣。

可是收益為正的投資必然是理性的么？

我們設想有這樣一種風險投資：若是當前的的資產為 S 的話，下一個單元時候的資產 50%的概率變為本來的 0.9 倍，50%的概率釀成本來的 1.11 倍。問題是：持續進行這樣的投資是否是理性的。

顛末簡單的計較可以獲得，顛末一個單元時候后，資產的數學期望是

$(0.9\times 0.5 + 1.11 \times 0.5) S= 1.005S$

，這樣預期收益為

$0.005S$

，也就是說，該投資單元時候的期望收益率為 0.5%。

也許看到這里你會感覺，不竭進行這樣的投資是無比理性的，看起來每一筆投資都無比的樂不雅。可是事實上，若是一小我不竭進行這樣的投資，他幾乎會滿盤皆輸。

我們用數學說話來描述這個問題：若是最初的資產是

$S_0$

，

$n$

個單元時候后的資產

$S_n$

是

$S_{n-1}$

的

$1+\eta_n$

倍，

$\eta_1,\eta_2,\dots$

之間是自力的，有 50%的概率為 0.11，50%的概率為 -0.1。那么

$S_n = S_0(1+\eta_1)(1+\eta_2)\dots(1+\eta_n)$

。

因為自力性，

$\mathbb{E}(S_n) = S_0\mathbb{E}(1+\eta_1)\mathbb{E}(1+\eta_2)\dots\mathbb{E}(1+\eta_n) = 1.005^nS_0$

。是以

$\lim_{n\rightarrow\infty}\mathbb{E}(S_n) = +\infty$

，也就是說理論上投資期望收益是正無限。

可是

$S_n = e^{\ln S_0 + \ln(1+\eta_1) + \ln(1+\eta_2) + \dots+\ln(1+\eta_n)}$

，

$\ln(1+\eta_n)$

有 50%的概率為

$\ln 0.9$

，50%的概率為

$\ln 1.11$

，所以

$\mathbb{E}[\ln (1+\eta_n)] = \ln 0.999 < 0$

。按照壯大數心猿意馬律，

$\mathbb{P}(\sum_{n=1}^\infty \ln(1+\eta_n) = -\infty) = 1$

，也就是說

$\mathbb{P}(\lim_{n\rightarrow \infty}S_n = 0) = 1$

，即幾乎可以必定不竭進行這樣的投資會血本無歸。

到這里讀者可能會發生猜疑，明明期望是正無限為何幾乎血本無歸呢？這是因為盡管

$S_n$

趨于零，可是

$\mathbb{E}S_n$

趨于正無限，就是說可能存在

$S_n$

很大很大，當然這種工作發生的概率很是很是小。成果導致很少的人賺良多的錢，可是絕大部門人血本無歸。

為了驗證這一不雅點，我利用蒙特卡洛方式進行了數值上的模擬。我一共模擬了一萬個投資者，初始資產都為 1，履歷了 300 個單元時候。模擬的成果如下：

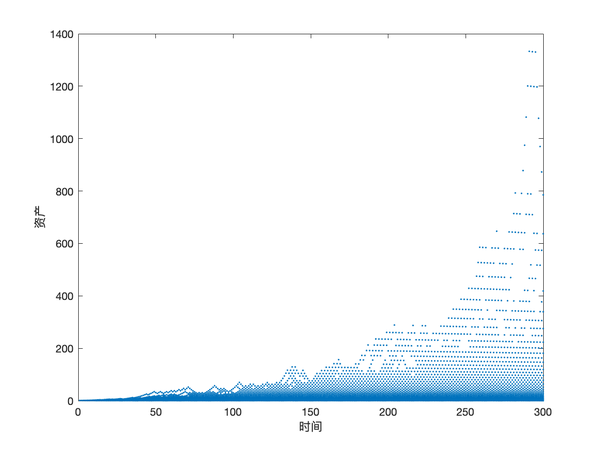
每一點代表了對應時候一個投資者的資產。我們可以看到，跟著時候的推進，越來越多的投資者的資產越來越少，可是與此同時，少少數投資者獲得了驚人的利潤。也就是說，固然社會總資產看起來是不竭增添的，可是背后埋沒的是社會上絕大部門的資產會把握在少少數人的手里，和絕大部門人會血本無歸。

這就是風險投資中的陷阱：看上去無比樂不雅的投資卻屢屢吃虧，明明理論上投資的期望收益是正無限，可是市場上幾乎沒有真正賺錢的投資者。

所以在賭場中，即使是一個賭神，可以或許做到每次賭錢的期望收益都是正的（這幾乎不成能實現），若是他賭性很大（每次都壓良多的錢，根基全壓）的話，到頭來也根基上血本無歸，真正可以或許經由過程賭錢賺錢的人是及其罕見的。

凱利公式

評論區 @Zhang Wang 提到了凱利公式，我也挺感樂趣，下面我就來繼續會商每次投資的時辰應該投資當前總資產的最優比例（倉位）

$F^*$

。

下面我們對遍及環境進行會商，收益率

$\eta$

從命某種分布而且知足

$\eta\geq -1$

，那么若是我們每次投資選擇的倉位為

$F$

的話，現實收益率變為

$F\eta$

，按照之前的會商我們知道，

$S_n^{1/n} = e^{\frac{\ln S_0 + \ln(1+F\eta_1) + \ln(1+F\eta_2) + \dots+\ln(1+F\eta_n)}{n}}$

，按照壯大數心猿意馬律

$S_n^{1/n}\mathop{\rightarrow}^{a.s.}e^{\mathbb{E}[\ln(1+F\eta)]}$

，也就是說平均收益率幾乎可以必定收斂于

$e^{\mathbb{E}[\ln(1+F\eta)]}$

，所以最優投資方案應該知足

$F^* = \mathop{\arg\max}\limits_{F\in [0, 1]}(\mathbb{E}[\ln (1+F\eta)])$

，令

$\phi(F) = \mathbb{E}[\ln(1+F\eta)]$

，

$\phi'(F) = \mathbb{E}[\eta/(1+F\eta)]$

，

$\phi''(F) = \mathbb{E}[-\eta^2/(1+F\eta)^2]<0$

。

若是

$\mathbb{E}[\eta]\leq 0$

的話，

$\phi'(F)\leq \phi'(0)\leq 0$

，

$\phi(F)$

關于

$F$

單調下降，所以

$F^* = 0$

，也就是說，在期望為負的投資中，最優選擇是一分錢都不投資。

若是

$\mathbb{E}[\eta] > 0$

的話，

$\phi'(0) = \mathbb{E}[\eta] > 0$

，因為

$\phi(F)$

是上凸函數，若是

$\phi'(1) = \mathbb{E}[\frac{\eta}{1+\eta}]\geq 0$

，申明

$F^* = 1$

，申明此時的最優選擇是倉位拉滿。

若是

$\phi'(1) = \mathbb{E}[\frac\eta{1+\eta}]<0$

，那么最優選擇知足

$\phi'(F^*) = \mathbb{E}[\frac\eta{1+F^*\eta}] = 0$

。

若是進行線性近似的話，

$0 = \mathbb{E}[\frac\eta{1+F^*\eta}] \approx \mathbb{E}[\eta - F^*\eta^2]$

，也即

$F^*\approx \frac{\mathbb{E}[\eta]}{\mathbb{E}[\eta^2]}$

。

對于最簡單的環境，

$\eta$

從命兩點分布，

$\mathbb{P}(\eta = t^+) = p$

暗示以概率 p 收益率為

$t^+$

，

$\mathbb{P}(\eta = -t^-) = q$

暗示以概率

$q = 1-p$

收益率為

$-t^-$

，此中

$t^+>0, -t^-<0$

別離暗示掙錢和吃虧的環境。

那么按照之前的闡發，投資有意義的充要前提為

$pt^+ >qt^-$

，在這種環境下，若是

$p \frac{t^+}{1+t^+} > q\frac{t^-}{1-t^-}$

，此時倉位拉滿。

不然，最優倉位知足

$p\frac{t^+}{1+F^*t^+} = q\frac{t^-}{1-F^* t^-}$

，化簡獲得

$F^* = \frac{p}{t^-} - \frac q{t^+} = \frac{pt^+ - qt^-}{t^+t^-}$

。這就是投資中的凱利公式。

當然可以直接計較

$F^* = \frac{p}{t^-} - \frac q{t^+} = \frac{pt^+ - qt^-}{t^+t^-}$

，若是

$F^*\leq 0$

，那么遏制投資；若是

$F^*\geq1$

，那么投資拉滿；若是

$0<F^*<1$

，那么每次投資總資產的

$F^*$

。

那么對于上文中提到的具體投資問題，

$F^* = \frac{5}{11}$

。

在這個問題下 @橫硯等 268 人提到了這個問題：

假設有一個游戲，人物的進犯力為 0～10，怪物的生命值為 10，不考慮防御、閃避、射中率等身分，那我平均進犯幾回可以殺死一個怪物？

@cyb 醬給出了用遞推解決了這個問題。我用直接計較的體例來計較這個概率。

我們把這個問題數學化，

$X_1, X_2, \dots, X_n, \dots$

是自力同分布隨機事務，代表人物每一次進犯造當作的危險，怪物的血量是 M ，那么需要進犯的次數

$T = \min\{t| X_1+\dots +X_{t}\geq M\}$

。求問：

$\mathbb{E}(T)$

。

因為

$T$

取值為正整數，所以

$\mathbb{E}(T) = \sum_{k=1}^{\infty}\mathbb{P}(T\geq k)$

。在這道題中，

$\mathbb{E}(T) = \sum_{k=1}^{\infty}\mathbb{P}(T\geq k) = \sum_{k=1}^{\infty}\mathbb{P}(X_1+\dots+X_{k-1} < M)$

。

分為兩種環境：

第一種環境是人進犯造當作的危險是持續的，也就是說是

$[0, M]$

之間的平均分布（

$X_i\mathop{\sim}^{i.i.d.} U([0, M])$

）。

另一種環境是人進犯造當作的危險是離散的，也就是說是

$\{0, 1,\dots , M\}$

上的平均分布。

第一種環境計較

$\mathbb{P}(X_1+\dots+X_{k-1}< M)$

顯然是一個幾何概型，對于

$k>1$

時，總樣區域對應著

$k-1$

維的邊長為 M 的立方體，而使得不等式當作立的區域是一個

$k-1$

維的錐體（二維時對應著直角三角形，三維時對應著三棱錐），體積為

$\frac{1}{(k-1)!}M^{k-1}$

，是以

$\mathbb{P}(X_1+\dots+X_{k-1}< M) = \frac{1}{(k-1)!}$

。

$\mathbb{E}(T)= \sum_{k=1}^{\infty}\mathbb{P}(X_1+\dots+X_{k} < M) = \sum_{k=1}^{\infty} \frac1{(k-1)!} = e$

。

第二種環境稍微復雜一點，計較

$\mathbb{P}(X_1+\dots+X_{k-1} < M)$

對應著一個古典概型，總事務數顯然是

$(M+1)^{k-1}$

。我們可以把

$X_1+\dots+X_{k-1} < M$

對應的事務拆分當作

$M$

個子互斥事務：

$X_1+\dots+X_{k-1} = s, s=0,1,\dots, M-1$

。

按照組合常識，

$X_1+\dots+X_{k-1} = s$

對應的事務數量為：

$\binom{s+k-2}{k-2}$

。所以

$\mathbb{P}(X_1+\dots+X_{k-1} < M) = \frac{\sum_{s=0}^{M-1}\binom{s+k-2}{k-2}}{(M+1)^{k-1}}= \frac{\binom{M+k-2}{k-1}}{(M+1)^{k-1}}$

。

$\mathbb{E}(T)= \sum_{k=1}^{\infty}\mathbb{P}(X_1+\dots+X_{k} < M) = 1+\sum_{k=2}^{\infty} \frac{\binom{M+k-2}{k-1}}{(M+1)^{k-1}} = (1+\frac1M)^M$

。對應

$M=10$

的成果為：2.59374246。

發表于 2019-08-06 23:33
閱讀 ( 1599 )
分類：其他類型

有哪些有趣的概率問題？

你可能感興趣的文章

相關問題

0 條評論

作家榜 ?

推薦文章