怎么用Matlab解方程？
使用matlab的solve指令來解方程是一條常用的指令。
東西/材料
matlab 2016a
操作方式
-
01
打開matlab，起首界說變量x：
syms x; -
02
matlab中solve函數的格局是solve(f(x), x)，求解的是f(x) = 0的解。
第一個例子，求解最常見的一元二次方程x^2-3*x+1=0:
solve(x^2-3*x+1,x)，解出的成果用切確的根式暗示。 -
03
matlab解出的根不僅包含實根，也包含復根，例如求解三次方程x^3+1=0:
solve(x^3+1,x)
我們知道該方程有一對共軛復根，matlab也可以解出它的解。 -
04
對于超出5次（含）以上的一元函數，有時無法用solve指令求的對應的根，如下圖所示。這時可以利用roots號令求解。roots號令的參數是方程的各個系數按高次冪到低次冪擺列當作的標的目的量，例如x^5+3*x^4-5*x^3+4*x^2-6*x+2=0，若是用solve指令獲得的成果不克不及令人對勁，而用roots就可以獲得對勁的成果。
-
05
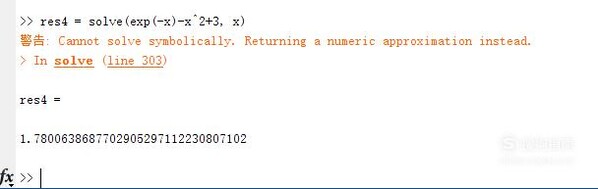
對于非多項式方程，只能利用solve求解。例如求解exp(-x)-x^2+3=0的解如下。經由過程黃色的警告可以看出，如許的方程沒有解析解，與我們已知的常識不異。
-
06
最后一類方程，是一元一次方程組。這是matlab最擅長的運算，可以利用矩陣進行求解。對于齊次線性方程來講，利用null(A,'r')。此中'r'暗示利用簡化階梯型行列式求解。對于如下的方程，可以解得線性無關的一組解。如許，我們還可以引入常量k1與k2表達通解。
-
07
對于線性非齊次的解，可以利用linsolve(A,b)。此中A是系數矩陣，b長短齊次項(若是b是多列矩陣，意味著解多個砼系數分歧齊次項的方程組)。對于圖中的方程組，可已如許求解。
- End
出格提醒
- 發表于 2018-02-11 00:00
- 閱讀 ( 786 )
- 分類：電腦網絡
admin
0 篇文章
作家榜 ?
-
xiaonan123
189 文章
-
湯依妹兒
97 文章
-
luogf229
46 文章
-
jy02406749
45 文章
-
小凡
34 文章
-
Daisy萌
32 文章
-
我的QQ3117863681
24 文章
-
華志健
23 文章