圖片：O12 / CCO 遙遠處所劍星，數學、物理、越野快樂喜愛者

宇宙大爆炸模子是當今被天文學家、宇宙學家、物理學家所普遍承認的關于宇宙成長轉變的模子。這個模子的提出是一大群物理學家配合盡力的當作果，并且后來還獲得了不竭的修補完美以及持續的驗證，可是“宇宙大爆炸”（Big Bang）這個名字倒是由一位極端否決宇宙大爆炸理論的天文學家、物理學家所提出來的，這個物理學家名字叫做弗雷德·霍伊爾。

霍伊爾也是一位卓有進獻的天文學家、物理學家，他與福勒等科學家配合提出的元素合當作理論，是諾貝爾物理學獎級此外當作果，但可惜的是，也許是因為與諾貝爾評獎委員會關系嚴重，1983 年福勒被授予諾貝爾物理學獎，可是霍伊爾沒能獲獎。霍伊爾在 1948 年與戈爾德等一路創立了“穩恒態宇宙模子”，而且果斷否決宇宙大爆炸理論。霍金當初到劍橋讀研究生的時辰，就很是想選擇霍伊爾作為本身的導師，可惜沒有實現。當然，霍金后來反而當作為了推翻霍伊爾穩恒態宇宙模子的主要“推手”。

1949 年 3 月，霍伊爾在加入 BBC 一個會商宇宙發源節目標時辰，嘲諷宇宙大爆炸學說，認為那種學說荒謬的將宇宙的發源付與一場“大爆炸”（Big Bang）。從此，大爆炸（Big Bang）就當作為了宇宙大爆炸學說的代名詞，到今天，已經當作為正式的名字了。

任何工作都是一把雙刃劍。“大爆炸”這個名字用爆炸來比方宇宙發源與成長轉變的理論，確實顯得活潑形象，從而在通俗蒼生中獲得了普遍的普及；可是，因為“爆炸”有著在日常糊口中切當的寄義，從而使得望文生義的吃瓜群眾們往往對宇宙大爆炸有著浩繁的曲解。好比，有人認為可以找到宇宙大爆炸當初起爆的那個點，并認為那邊就應該是宇宙的中間；有人認為既然是爆炸，那么必然有一個爆炸圈的最外層，認為那邊就是宇宙的鴻溝；還有人傳聞膨脹的宇宙可以超光速，在知乎上還問出過這樣的問題“若是我能抓住宇宙膨脹的邊緣，那么是不是我就可以超光速活動了？”；......

所以說，一個名字有時也會帶來良多不測的麻煩。宇宙大爆炸理論其實挺復雜，涉及到宇宙從發源到今天的成長演變的全過程，并且有良多尚待解決的問題。今天，我們不談那么多復雜的工作，而只是談一件事，宇宙到底是怎么“爆炸”的！

一、一切的“始作俑者”恰是愛因斯坦的廣義相對論

在廣義相對論呈現以前，我們是沒有能力用科學方式去研究宇宙的，那時辰所有對于宇宙的研究都是哲學思慮。一個原因是那時沒有足夠的不雅測能力，連銀河系還看不全呢，當然不領會整個宇宙會是什么樣子；第二個原因是沒有理論根本，從而無法用科學理論來指導研究宇宙。廣義相對論呈現今后，人們終于有了可以在大標準上描畫宇宙時空圖景的理論。

在研究宇宙之前，人們老是要有一些根基假設，我們稱之為“宇宙學道理”。這個道理固然名字很有氣焰，可是內容只有一句話：每一時刻的宇宙空間在大標準上是平均且各標的目的同性的。這個假設是如斯的天然，并且也合適我們今天的大標準天文不雅測，從而被認為是宇宙學研究的基石。

可別小看這一句話，這個道理的當作立使我們研究宇宙時候和空間的時辰省了大事兒了。當然，嚴酷地推導涉及到復雜的微分幾何與廣義相對論常識。粗略上說來，每一時刻的空間平均意味著我們宇宙四維時空中存在著平均面族（這個“面”指的是四維時空中的三維超曲面），各標的目的同性則意味著存在各標的目的同性參考系，我們再加上一個很是天然的假設，也就是平均面族是獨一的，從而可以證實各標的目的同性參考系中任一各標的目的同性不雅者的宿世界線與這個獨一的平均面族正交，還可以證實肆意兩個平均面之間的各標的目的同性不雅者的宿世界線長度不異。于是，我們可以把這個一族三維超曲面組成的平均面族稱為“空間”，把各標的目的同性不雅者的固有時稱作“時候”，把各標的目的同性參考系稱為宇宙靜系，從而一勞永逸的解決了我們宇宙的“時空 3+1”分化問題。【若是沒有這個根本，我們在研究宇宙的時辰連如何劃分時候和空間可能都難以做到，這是廣義相對論中較復雜的一部門常識，與人們日常糊口中自然能區分出時候和空間的感觸感染很不不異】

有了上面的根本，我們才能談論宇宙的春秋、星系間的距離、可不雅測宇宙的半徑等等概念，不然時候、空間都是相對的，沒有上述根本我們是無從談起的。

二、三種可能的宇宙空間及其是若何“爆炸”的

在宇宙學道理的根本上，基于微分幾何推導，結論是：對于任一時刻，我們宇宙的空間只可能有三種環境——常正曲率空間、平直空間和常負曲率空間。是的，只需要用到宇宙學根基道理，我們就可以獲得這樣清楚的結論。

不領會空間可能會彎曲的伴侶也許會迷惑，這幾種空間到底是什么意思？其實，因為任何空間在極小的規模內都高度近似為平直空間，放在宇宙標準來看，我們人類就糊口在一個極小的規模內，導致人們從起頭進行幾何學研究的時辰，從沒想到過空間還可能是彎曲的。歐幾里得在撰寫《幾何原本》的時辰，把“過直線外一點有且只有一條直線與已知直線平行”作為了一個正義，就是將空間的平直性看做自然當作立的了。無論是歐幾里得，仍是后來的很多數學家，都沒有熟悉到空間的平直并不是必然的。直到高斯，尤其是其學生黎曼的進獻，才讓人們知道了，本來空間也可所以彎曲的。

從愛因斯坦的廣義相對論頒發起頭，人們逐漸加倍理解到，空間不僅僅是可以彎曲的，其實我們糊口的空間和時候（四維時空）真的就是彎曲的。

怎么理解空間的彎曲呢？最好的法子就是站在一個更高的維度上去不雅察低一個維度的空間，這樣就很輕易看出其彎曲的特點。好比，球面就是一個彎曲的二維空間，但若是你是一個糊口在球面上的二維生物，你很難熟悉到這一點，而像我們這樣糊口在三維空間的生物則相對輕易發現球面是一個彎曲的二維空間。但即使是糊口在三維空間中的我們人類，面臨一個龐大的二維球面的時辰，也往往熟悉不清，這樣的例子在人類汗青上是真實發生過的，人們直到 400 年前麥哲倫舉世航行后，才確信地球是圓的，在這之前，絕大部門人都認為地球是平的。看，固然我們是三維空間中的生物，可是面臨一個如斯龐大的二維球面，我們也花了 4、5 千年的時候才熟悉到這個概況是彎曲的（從人類呈現文明算起）。所以，對于一個二維生物來說，幾乎沒有可能熟悉到他們糊口的二維空間是彎曲的。同樣，作為糊口在三維空間中的生物的我們，熟悉到空間是彎曲的，是一個極為了不得的事務，這也恰是愛因斯坦為什么如斯偉大的原因！

1、第一種可能——常正曲率空間

合適宇宙學道理的常正曲率空間其實就是一個平直四維空間（注重不是四維時空）中的三維超球面。這很近似于一個平直三維空間中的二維球面（這個我們通俗人都能理解）。所謂常正曲率，意思就是空間曲率為一個正的常數。這樣的空間是一個封鎖的空間。

我們知道，在三維直角坐標系（三維笛卡爾坐標系）中，二維球面的方程為

畫出來就是一個半徑為 R 的球面。同樣的，在四維直角坐標系中，三維超球面的方程為

此中的

就是四維空間中的四個坐標值組成的一個點。這個三維超球面我們無法繪制出來，也無法建造一個立體三維模子把它表達出來，因為我們糊口的三維空間中沒有第四個維度可以供這個三維超球面來彎曲。

若是宇宙是常正曲率空間，宇宙大爆炸指的就是三維超球面的半徑 R 從 0 起頭變大的過程！這樣，R 就當作為了時候（就是宇宙靜系中各標的目的同性不雅者的固有時）的函數，我們一般設

。

我們無法繪制出三維超球面，可是我們可以把這個三維超球面壓縮 1～2 個維度來類比，這樣也可以讓伴侶們對這種環境下的宇宙大爆炸有個感性熟悉。

（1）壓縮兩個維度來描述

若是把三維超球面壓縮 2 個維度，也就是令

，三維超球面就退化為一維的圓周。若是這樣的話，宇宙大爆炸的示意動圖如圖 1。

圖 1 把三維超球面壓縮 2 個維度，示意宇宙爆炸的過程。

在圖 1 這個示意中，那一個維度的圓周就是我們糊口的宇宙，注重這時我們半斤八兩于糊口在一條曲線上的一維生物。若是你必然要問宇宙大爆炸的起爆點在哪里，我只能說起爆點在圓心處，可是很遺憾，圓心這個點不在圓周上，換句話說，起爆點不處于我們糊口的空間之中！圓周上被標出的 8 個點，可以認為是宇宙中的 8 個星系，很顯然，固然它們本身沒有彼此活動，可是他們之間的距離卻在不竭增添，這也就是為什么星系之間都在互相遠離的原因。

（2）壓縮一個維度來描述

若是我們把三維超球面壓縮 1 個維度，也就是令

，三維超球面就退化為二維球面。若是這樣的話，宇宙大爆炸的示意動圖如圖 2 所示。

圖 2 把三維超球面壓縮 1 個維度，示意宇宙爆炸的過程。

在圖 2 的示意中，那個球面就是我們糊口的宇宙，這時我們半斤八兩于糊口在一個二維球面上的二維生物。同樣的，球心作為最合理的起爆點，也不在二維球面上。在這個二維球面上，我們若是朝著一個偏向一向沿直線活動下去，不考慮空間在膨脹的身分，總有一天我們會回到起點，正如麥哲倫舉世航行一樣。這個特點是常正曲率空間的一個典型性質。所以，固然我們作為三維空間中的生物可以很清晰的看到這個球面在膨脹變大，可是若是是糊口在球面上的二維生物們，顯然是不會發現本身所糊口的空間存在“鴻溝”的！

（3）不壓縮維度來描述

因為我們無法繪制三維超球面，所以很遺憾，這時辰我們畫不出圖來了。為了更好的理解這種宇宙空間的特點，可以給出三維超球面中的兩個事實，會對想象這樣一個四維空間中彎曲的三維超球面有一些幫忙：

事實 1 ：與二維球面一樣，在三維超球面中，若是我們朝著任一個偏向一向沿直線活動下去，不考慮宇宙的膨脹，總有一天我們會回到起點。關于這一點，我無法繪圖表達，大師可以自行腦補，或者用低維度的環境做參考。

事實 2 ：在二維球面上，若是我們繪制一個圓周，這個圓周其實會有兩個圓心和兩個分歧的半徑，如圖 3 所示；同樣的，在三維超球面上，若是我們繪制一個球面，這個球面也有兩個球心和兩個分歧的半徑，如圖 4 所示。

關于事實 2 乍一聽到不輕易理解，我這里多詮釋下。先說二維球面，圖 3 中的以 O 為球心的二維球面上繪制一個圓周（橙色虛線圓周），在我們三維空間中的人看來，這個圓周的圓心當然在點 K 處，半徑為 KC=r，可是別忘了，點 K 不屬于二維球面。所以，在二維球面上的二維生物看來，這個圓周的圓心既可以在 E 點，此時半徑為“圓弧 EC”（橙色實線圓弧）；圓心也可以在 F 點，此時半徑為“圓弧 FC”（綠色實線圓弧）。可見，彎曲的二維球面上的圓周，半徑很大之后，圓的周長反而可能很小。

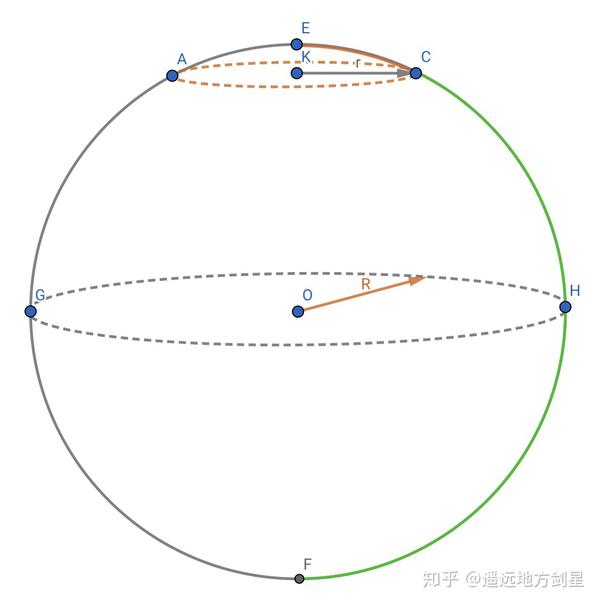圖 3 二維球面上的橙色虛線圓周其實有兩個圓心 E 和 F，有兩個半徑“弧 EC”和“弧 FC”

回到我們糊口的三維空間，若是我們的宇宙確實是常正曲率空間的話，也會有近似的現象。如圖 4 中以 A 為球心繪制一個半徑為 r 的球面，點 C、P、D、Q 都是球面上的點。那么在我們的宇宙中必然存在著別的一個點 S，這個點到球面上各點的距離也都一樣，只不外這個距離可能會很大。圖 4 只能是一個示意，因為我們無法畫出真實的環境，原因是我們空間的維度不敷。

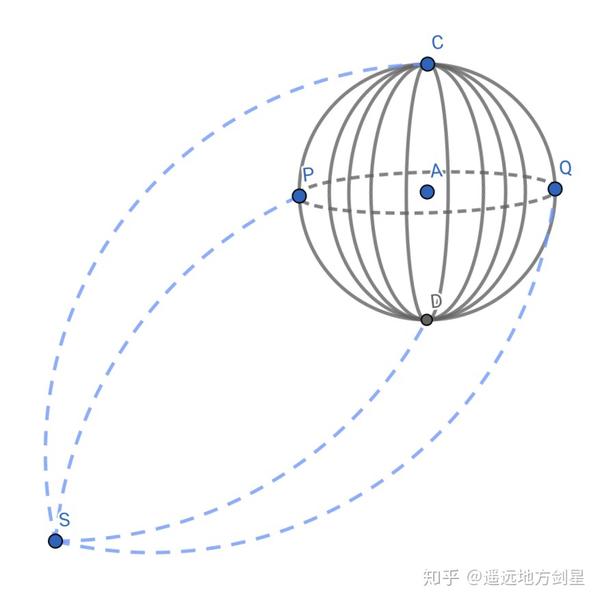圖 4 在三維常正曲率空間中繪制一個以 A 為球心、AC=r 為半徑的球面，那么空間中也必然存在別的一個點 S 也是這個球面的球心，S 到 C、P、D、Q 等球面上個點的距離 R 也都相等，只不外若是 r 很小的話，R 會很大。

換個更形象的說法，當我們捧著一個地球儀的時辰，我們本身認為這個地球儀的球心在我們手的掌控之中，可是若是我們的宇宙是常正曲率空間的話，我們就應該知道，在很遙遠的處所必然存在著別的一個點，這個點也是你手中地球儀球面的球心，并且相對這個球心來說，你手中的地球儀球面半徑大的驚人，起碼跨越 460 億光年，甚至可能跨越 1000 億光年。

2、第二種可能——平直空間

這種可能是最簡單的一種環境。在這種環境下，我們的宇宙就是一個尺度的平直歐幾里得三維空間，只不外處于膨脹過程中。固然在不竭膨脹，可是任一時刻，我們宇宙的空間都是平直的三維歐氏空間。壓縮一個維度后，這種宇宙大爆炸的示意動圖如圖 5 。

圖 5 壓縮一個維度后，平直空間宇宙大爆炸示意動圖

伴侶們可能會有疑問了？圖 5 示意的哪像大爆炸啊？不就是一個平均的平面被平均的拉伸嗎？為領會釋這種環境下的宇宙大爆炸，我們不得不請出宇宙學研究中最根本的“羅伯遜 - 沃克”度規（RW Metric）。這個宇宙的線元長度表達式如下，

上式第一個等號右邊是用平面直角坐標系暗示的，第二個等號右邊是用球坐標系暗示的，但本色都是一樣的。最關頭的一點是空間線元前面的系數

。在前面介紹第一種環境常正曲率空間的時辰，我們提到了

就是三維超球面的半徑。可是在第二種環境中，

不再有這樣的寄義，它只是一個隨時候轉變的系數罷了。

問題是這個

在

時，

。從而我們可以計較獲得，

的時刻，空間線元長度恒為 0 。這也就意味著 t=0 這個時刻沒有空間。可是，只要

，不管

此時是何等小的正數，空間線元就籠蓋了全數的三維坐標，當作為了一個無限大的三維歐氏空間。從這個意義上講，這種環境下的宇宙大爆炸只是在

這個奇點處宇宙空間才不存在，只要一起頭“爆炸”，無限大的三維平直歐氏空間就降生了。所以，我們的示意圖只能是這個樣子啦。

這種環境下，連疑似的起爆點我們都找不到，看到的就是一個無限大的三維歐氏空間在不竭膨脹罷了。

3、第三種可能——常負曲率空間

我們泛泛很少接觸負曲率空間，所以對于這種環境可能更不熟悉。這種環境下，宇宙的任一時刻，空間都曲直率為負的常數的彎曲空間。這種負常數曲率空間其實就是平直四維空間中的三維超扭轉雙曲面，可以類比為平直三維空間中的二維扭轉雙曲面。這種負曲率空間并不封鎖，是一個開放的空間。

二維扭轉雙曲面的方程為

近似的，三維超扭轉雙曲面的方程為

同樣因為維度的原因，我們無法畫出這種三維超扭轉雙曲面的樣子。仍是近似第一種環境，經由過程壓縮維度，來給大師一些感性熟悉。

（1）壓縮兩個維度來描述

若是令

，獲得的方程很簡單，就是一條雙曲線。我們知道雙曲線分為互不連通的兩部門，我們只取

的部門，因為此時這條雙曲線就代表了我們糊口的一維空間，而我們顯然只能糊口在連通的空間中，另一條不連通的曲線與我們沒有任何干系。

此時的宇宙大爆炸其實就是

從 0 起頭增大的過程，這種環境下的

，看起來的樣子如圖 6 。

圖 6 常負曲率空間壓縮兩個維度后，宇宙大爆炸示意圖。

請注重，在

的時辰，雙曲線退化為兩條

角的折線，也就是

的圖像。所以，這種環境下的宇宙大爆炸，其實是從兩條折線所代表的一維空間起頭膨脹的過程。當然，空間是兩條折線的時辰，折點處的空間是持續但不成導的，這種空間也同樣是不成理解、不該存在的，所以，這也是大爆炸奇點可能的一種形態。

跟著空間的膨脹，整條曲線還沿著

軸在上升。可是，要知道，

坐標軸是一個我們無法觸碰的維度，所以，作為糊口在這條曲線上的一維生物，我們無從感知曲線在某個其它維度的上升。可是，曲線上標準的膨脹仍是顯然的，這叢所標心猿意馬的多個點逐漸在分手就可以感觸感染到了。

（2）壓縮一個維度來描述

近似的，若是壓縮一個維度，令

，三維超扭轉雙曲面就退化為二維扭轉雙曲面。這時宇宙大爆炸的動圖如圖 7 所示。

圖 7 常負曲率空間壓縮一個維度后，宇宙大爆炸示意圖。

這種環境下的宇宙大爆炸是從一個圓錐面起頭的，“起爆點”，也就是大爆炸奇點，是一個無限大的圓錐面。這種環境下，若是我們固心猿意馬

，獲得的

平面（這顯然是一個與

坐標面平行的平面）與扭轉雙曲面的交線是一個半徑為

的圓周。所以，我們也可以認為，這個雙曲面是由無數條這樣的圓周在

維度上移動組合而當作的。

（3）不壓縮維度來描述

這下可難了，我們即畫不出圖來暗示真正的三維超扭轉雙曲面，也沒法舉出太有用的有助于理解的例子。參照壓縮一個維度的說法，也許可以這樣想象這種空間：

固心猿意馬某一個

之后，獲得的

三維超平面（這個三維超平面其實就是四維歐氏空間中的某一個三維歐氏子空間）與這個三維超扭轉雙曲面訂交獲得的二維曲面是一個半徑為

的球面，可是要注重，這個球面的球心卻不在我們所處的三維超扭轉雙曲面空間之內。那么，我們這個三維超扭轉雙曲面空間其實就是由無數個這樣的球面在

維度上移動組合而當作的。

嗯，作為三維空間中的生物，硬要去想象四維空間中的場景，難度是很大的。有的人甚至說這是不成能的。說真話，我也想象不出這樣的三維超扭轉雙曲面到底是什么樣子，因為我們都從來沒有過第四個空間維度的體驗。所以，最后只能經由過程數學計較來理解這些抽象的概念了。

三、關于宇宙大爆炸的幾個問題

有了上面描述的根本，再往返答下面的一些問題，就相對輕易了些。

1、宇宙有中間和鴻溝嗎？

謎底是——沒有。

這其實從宇宙學道理就可以獲得。宇宙學道理告訴我們，任一時刻的宇宙都是平均的和各標的目的同性的。那么顯然，若是有中間，或者有鴻溝，都意味著在宇宙中存在一些位置比其它位置更特別，這當然是違反宇宙學道理的。所以，這個問題的謎底很是明白。

多說一句，在第三種環境“常負曲率空間”下，似乎那個壓縮一個維度后的扭轉雙曲面有一個中間啊？但那只是我們站在更高維度上看到的一種情境，而作為身處二維扭轉雙曲面內的二維生命來說，它們是感觸感染不到存在中間的。這是因為對曲面上任一點，都存在著這樣一種等度規的映射，對這個點來說是恒等映射，可是卻可以讓這個點的任一矢量扭轉任一要求的偏向和角度。仍是那句話，只有經由過程數學計較，才能理解這些抽象的性質。

2、大爆炸奇點到底是什么？

謎底是——可能是一個點，也可能是一個不成導的無限大空間。

這顯然取決于我們的宇宙到底是三種環境中的哪一種。對于第一種環境，可以認為是一個點，或者認為是一個半徑無限小的三維超球面；對于第二種環境，可以認為是一個點，也可以認為就是一個無限大三維歐氏空間；對于第三種環境，只能認為是一個不成導的無限大三維退化超扭轉雙曲面。

但不管怎么樣，都可以經由過程某種坐標轉變，把大爆炸奇點變換當作為一個三維類空超曲面。所以，萬萬不要再把大爆炸奇點簡單地輿解為一個點了，其實大爆炸奇點和我們凡是意義上的一個點很不不異。

3、宇宙巨細有限嗎？

謎底是——可能有限，也可能無限。

這也取決于我們的宇宙到底是哪種環境。

第一種環境下的宇宙體積是有限的，我們可以經由過程微分幾何計較獲得這種三維超球面的體積，成果是

。顯然，跟著宇宙的膨脹，

的增加，宇宙的體積也會增加。當然，宇宙是否會永遠膨脹下去，這還需要進一步研究。

第二種環境和第三種環境的宇宙空間都是開放的，不封鎖的，顯然體積是無限大的。

可是不管宇宙體積是否有限，宇宙必然都是無中間、無鴻溝的。

4、為什么會有可不雅測宇宙與不成不雅測宇宙的區分？

這個問題本文篇幅有限，只能簡單申明一下。

起首，宇宙大爆炸剛起頭的時刻，物質和能量堆積在一路，處于超高溫度、超高壓強下，光子是無法自由穿梭的。也就是說，在宇宙大爆炸起頭后的一段時候，宇宙是不透明的。大要從宇宙大爆炸發生 40 萬年后，光子退藕（退出耦合的意思），宇宙才被認為是透明的。這個時辰某些位置的光子顛末很長的時候，終于跑到了我們今天的視野里，這被認為是我們可以或許看到的最早的光子。我們知道宇宙的春秋大要是 137 億年，那么這些到我們眼里的最早的光子顯然奔馳了 137 億年（一起頭那 40 萬年太小，就忽略不計了）。可是，跟著宇宙的膨脹，那時這些光子發出時刻的位置今天已經膨脹到離我們更遠的處所了，我們所說的可不雅測宇宙的半徑，指的就是這些光子發出時刻的位置今天離我們的距離，顛末復雜的計較，人們估量它們今天離我們大要 460 億光年。這就是可不雅測宇宙半徑在今天的值。跟著宇宙的膨脹，跟著時候的增加，可不雅測宇宙半徑還會轉變。今朝看來，顯然還會繼續變大；至于最終會如何演變，這取決于我們宇宙到底是哪種空間景象，又是若何繼續膨脹的，這是一個需要深切研究的課題。

5、到底宇宙是三種空間中的哪一種呢？

謎底是——這個問題現在還沒有切當謎底。

可是我們可以有一些猜測。按照宇宙學道理和愛因斯坦廣義相對論的推導，我們可以獲得一個宇宙學的恒等式，

，此中

，

是當今的哈勃常數（其實就是我們前面說的函數

在當今時刻的值），

是萬有引力常數，

是當今時刻宇宙中物質的密度，

是當今時刻宇宙中輻射的密度，

就是赫赫有名的宇宙學常數（就是我們今天也米有搞清晰的暗能量的來歷，有時也叫做真空能量密度參數），

就是

在當今時刻的值，

則是用來標識我們宇宙到底是三種環境中的哪種的指標，

代表常正曲率空間，

代表平直空間，

代表常負曲率空間，

只有這三個取值。

宇宙學家和天文學家按照大量不雅測，估量出了上面除了

以外的其它參數，固然有些很不切確，可是帶入上面的恒等式獲得的成果似乎表白，

接近 0 。也就是說，我們可以按照今朝不雅測成果猜測，我們的宇宙在大標準上很可能是平直的三維歐氏空間。

當然，除了這些不雅測，我本人還甘愿答應給出別的一種猜測。那就是，究竟結果三維以上更高的維度我們誰都沒有見過，若是利用奧卡姆剃刀，“不增添沒有需要的實體”，那么我們可以猜測原本就沒有第四個空間維度。從而，我們也許可以認心猿意馬

，宇宙在大標準上就是一個平直的三維歐氏空間。當然，這是我本人的癡心妄想，僅供參考，萬勿當真。

?

宇宙就是這樣爆炸的，不要再去探尋宇宙的鴻溝、宇宙的起爆點了，我們的宇宙也許是一個有限而無界的空間，更大的可能是一個無限而無界的空間。我們人類糊口在此中，細微的連一粒塵埃都遠遠算不上，可是，我們人類偉大之處在于，我們知道這個宇宙可能是什么樣子的，這也許是宇宙賜賚我們人類最大的幸福！