1+2，陳景潤早已證明出來，如何證明1+1？

在一些有關數學的文章中，我們經常會看到中國數學家陳景潤當作功證實了“1+2=3”，而全宿世界沒有一個數學家可以或許證實“1+1=2”。然而，事實并非如斯。

無論是“1+2=3”，仍是“1+1=2”，都是數學正義，始終都是當作立的，這都是成立在皮亞諾正義之上，證實這樣的恒等式沒有意義。數學家真正要證實的是哥德巴赫猜想，這一向是當今數學界所未解決的一浩劫題，大數學家大衛·希爾伯特曾將其列為23大數學難題之一。

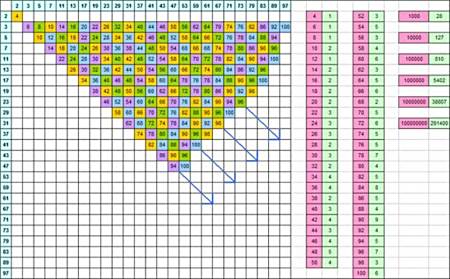
哥德巴赫在1742年給歐拉寫的一份信中提出了一個猜想——對于肆意一個比2大的偶數，即4及以上的偶數，它都等于兩個質數（或稱素數）之和，這就是所謂的“1+1”。也就是說，大于2的偶數可以拆分當作至少一對證數，例如，8=3+5，14=3+11=7+7。

在那時，即即是歐拉也無法證實哥德巴赫猜想。此外，還有高斯、黎曼等數學家研究過哥德巴赫猜想，但也都沒有證實出來。不外，有了這些數學家孜孜不倦地盡力和支出，為后來數學家的進一步研究打下了堅實的根本。

因為哥德巴赫猜想一向無法被直接證實出來，所以數學家另辟門路，經由過程證實哥德巴赫猜想的推論來逐漸接近這個猜想。迄今為止，我國聞名數學家陳景潤是最接近證實哥德巴赫猜想的人，他證實了“1+2”。

陳景潤證實，對于肆意一個足夠大的偶數，它可以用兩個質數，或者一個質數與一個半質數的和來暗示。半質數可以用兩個質數之積來暗示，例如，21是一個半質數，它可以暗示為質數3和質數7的乘積。這個定理被稱作陳氏定理，也就是凡是所說的“1+2”。為了證實“1+2”，陳景潤足足用了幾麻袋的草稿紙，這樣的當作就在沒有計較機幫忙的時代十分令人佩服。