【MATLAB】多項式的四則運算和微積分運算

多項式之間可以進行四則運算，結果仍然為多項式。在MATLAB中，通過系數向量進行計算，結果仍為系數向量。本經驗中所用MATLAB軟件版本為R2020a。

東西/原料

1
多項式的加減運算。沒有相關的函數，現實上加減運算就是系數標的目的量的加減運算，只要將系數對其即可。
2
多項式的乘法運算。利用conv函數實現，挪用格局為：
p=conv(p1,p2)
3
多項式的除法運算。利用deconv函數實現，挪用格局為：
[q,r]=deconv(p1,p2)，此中q為商式，r為余式。
4
多項式的微分。利用polyder函數，挪用格局為：
p=polyder(p1)，求多項式p1的導數；
p=polyder(p1,p2)，求多項式p1*p2的積的導數；
[p,q]=polyder(p1,p2)，p1/p2的導數，p為導數的分子多項式系數，p為導數的分母多項式系數。
5
多項式的積分。利用polyint函數，挪用格局為：
I=polyint(p,k)，求以p為系數的多項式的積分，k為積分常數項；
I=polyint(p)，求以p為系數的多項式的積分，積分常數默認為0。
6
多項式部門分式睜開。利用residue函數，挪用格局為：
[r,p,k]=residue(B,A)，B為分子多項式系數標的目的量，A為分母多項式系數標的目的量，k為余式多項式行標的目的量。p為頂點列標的目的量，r為零點列標的目的量。
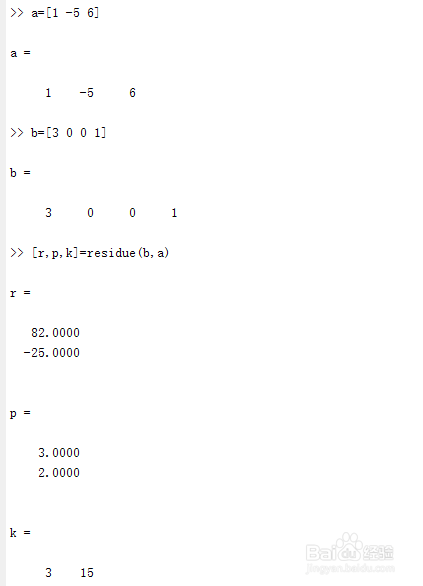END