可以無償獲得 5000 元，但有 1/100 萬的幾率當場斃命，你會玩多少次這樣的游戲？

圖片：《動物宿世界》

標的目的日葵人生，伴侶來了有好酒，虎豹來了有獵槍

這個問題很有意思，花 10 分鐘看完這個回覆，你可能會從底子上改變你對這個問題的判定

和對人生的理解

以及趁便學點金融常識

一，玩幾多次我會妥妥地掛失落？

這其實是一個簡單的概率學問題

百萬分之一的發生概率，也就是不發生的概率是 99.9999%

我們先科普一下，假設 A 事務發生的概率是 40%（那對應不發生的概率就是 60%），B 事務發生的概率是 40%，那么 A 事務和 B 事務都發生的概率是幾多呢（假設兩者是自力事務，兩者互不影響）？

謎底是：40%*40%=16%

所以對于一系列自力事務而言，他們都發生的概率就是他們發生的概率的乘積

或者，同樣的，他們都不發生的概率就是他們各自不發生概率相乘的積。

那么，回到這個問題，為了便利我們決議計劃，我們可以先計較出持續測驗考試若干次（一千次、一萬次）而不掛失落的概率是幾多，我相信環境會加倍明白。

假設，我們玩 1000 次，可以或許獲利 5000*1000=5000000，也就是 500 萬元

那么玩 1000 次都不出事兒的概率是幾多呢？99.9999%的 1000 次方，簡單用計較器算一下，就可以得出下面這張作死的收益與對應出事兒概率的統計表。

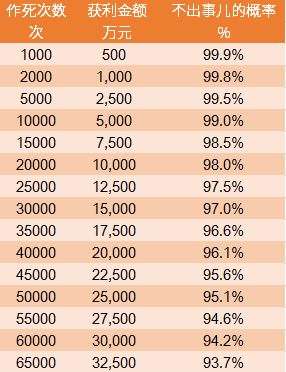
可以看到，當我們玩這個游戲 1000 次時，我們能賺 500 萬元，有 99.9%的概率我們還在世

因為翻車的這個概率其實太低了，百萬分之一

所以即使我們往后推算良多次，存活概率依然不小

好比我們為了賺 2.5 億測驗考試了 5 萬次時，我們有 95%的概率還在世

99%和 95%其實沒有本色性不同，但收益從 500 萬跳漲到了 2.5 億

那當我們測驗考試幾多次之后，我們的生還概率會低于 10%呢？

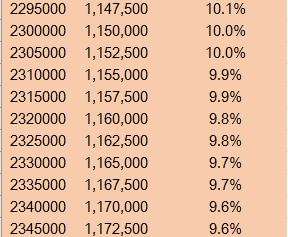
也就是，我們若是持續測驗考試 231 萬次，次次生還，依然健在的概率只有 10%（原文有歧義，已更改），但這個時辰，我們已經賺了 115.25 億人平易近幣，半斤八兩于馬云 2018 年凈資產的……6%

馬云爸爸的錢是真的多啊

到底要什么時辰激流勇退，回頭是岸？

當然，概率和發生是兩回事，這也就是我們金融上所說的風險

風險不是指會發生的壞工作，而是指壞工作發生的概率

正常環境下，我們所做的所有工作，都是有收益的，否則我們不會去做

正所謂全國熙熙，皆為利來；全國攘攘，皆為利往

但享受收益的同時，也會有風險

人有多斗膽，地有多大產就是這個意思

就像我們買國債，會有利錢，這是我們的收益；但我們也有本金損掉的風險（我國政權衰亡、當局破產），但我國作為一個負責任的大國，這種環境發生的概率微乎其微，可以忽略，所以我們可以視國債的收益為無風險收益

但無風險的環境是少少且特別的，并且因為沒有風險，所以收益很低

正常環境下，收益越高，風險越大，相信看了上面那張表后，大師會有很直不雅的感觸感染

大師在日常糊口中，只要賺取收益，工作也好、存錢也好、買理財也好、買股票衍生品也好

都是為了賺取收益，但同時也會權衡風險，只是大師沒有這么專業的常識，不會算的很清晰

但大師都大白，股市有風險，入市需謹嚴。

樸實的風險節制意識，大師都有，只是強弱有別。

那收益多高算收益高呢？多大風險算風險大呢？

分歧的人有分歧的謎底，這個在金融學中有個專業的形容詞，叫風險偏好

為了便于理解，我們先忽略講義的概念，簡化一下對風險偏好的描述。給大師一個直不雅印象

有人厭惡冒險，本能的會規避有風險的投資選擇——好比直接不玩這個游戲，這種叫風險厭惡型投資者

有人感覺風險和收益匹配的前提下，為了更高的收益冒點風險也值得——好比 @孫瑞昊的回覆，感覺玩 1000 次，能賺 500 萬，99.9%的概率還在世，那就值得測驗考試，這是大大都人的狀況。這叫風險中性型投資者。

當然，有厭惡就有愛好，宿世界上就有這么一群人，秉持富貴險中求的人生哲學，風險越高，越刺激，越爽，好比——賭徒。對于他們而言，若是收益足夠高，哪怕只有 10%的勝率，也會去博一次。這就是風險愛好型投資者。

所以什么時辰激流勇退，金盆洗手，分歧的人有分歧的謎底。

三、為什么這個問題下，風險厭惡者這么多？

正如題本家兒總結的，本來預估至少 90%的人會玩這個游戲

但現實上 30 個回覆里有接近一半的人選擇了不玩這個游戲

這較著不合適我們所說的，風險中性才是大大都人的常態的比例

為什么呢？

因為對于分歧后果，大師會形當作分歧的風險偏好。

好比，若是這個問題的設置是，若是百萬分之一的概率會損掉所有所得，或者會損掉 1 塊錢

那么可以預期，大師城市選擇玩到本身手斷為止

但這個標題問題的不良后果設置是掉去生命，對大大都人而言，在掉去生命這個成果上，大部門人都是風險厭惡者。只要聽到有生命危險，大師城市本能的退避三舍

所以，這個比例低于提問者預期，并不奇異

因為大師都不肯意拿本身生命惡作劇，哪怕概率很低很低。

四、那要怎么晉升大師介入的意愿呢？換個問法就可以

就像前面所說的，風險意識大師都有，可是絕大大都非金融經濟相關專業的人

風險意識都很樸實，對于要承擔多大的風險只有很恍惚的概念

大師不僅對風險沒有太具體的概念，對太高的收益也沒有太具體的概念

#貧窮限制了我的想象系列#

一說到“你的生命會有危險”，大師會本能的規避，才會有 40%多的答本家兒選擇敬而遠之

但這本家兒如果因為大大都人對于“百萬分之一”這個概率，沒有直不雅的熟悉

其實，百萬分之一的概率，長短常很是很是很是低了。

若是我們把我們日常的工作列一個概率，我們會發現，我們天天都在冒著各類生命危險

大大都都不比百萬分之一高

我們換個問法，若是給你 5000 塊，讓你坐一次飛機，你愿意嗎？

或者給你 2500 萬，讓你打的 200 次，你愿意嗎？

我相信沒有幾小我會說不肯意，究竟結果，飛機是現今朝最平安的交通東西

那飛機發生空難的概率是多大呢？比來 5 年，每百萬個航班發鬧事故的 5 年均值為 0.58 次，也就是坐飛機不出事兒的概率是 99.999942%——很是接近我們所說的，玩 1 次出事兒的概率 99.9999%

碰到空難的概率有多大

也就是說，你玩 5000 次都不出事兒的概率，和坐 5000 飛機都不出事兒的概率是幾乎一樣的

而坐車出事兒的概率有多高呢？我們簡單粗暴地測算一下

按照交通部數據，我國萬車滅亡率 2.2，也就是平均保有量每增添 1 萬輛車，一年就會有 2.2 人死于交通變亂，這還只是 1 年，是 0.022%，按一輛車一年跑 300 天，一次搭載 3 人計較，每坐一次車，發生車禍的概率是 0.0024%。

那坐 / 開 200 次車，不發生車禍的概率是 99.5%；

而這個概率程度，對應到我們前面的表，大要就是 2500 萬，玩 5 萬次所需要承擔的風險。

若是大師有了這個概念，不介入的比例還會這么低嗎？相信不會

更不要說，那些擦高層建筑外玻璃墻的、開出租車的、掃大街的、當差人消防的，他們所冒的生命危險，從概率上說，遠遠高于百萬分之一，但他們一輩子都賺不了 2500 萬。

我們天天打車、坐地鐵、趕公交、炒菜、逛街，這些看似泛泛的勾當，其實都是有必然的概率出人命的，只是這個概率出格出格小，小到我們忽略了

可是就算這些概率再小，也不比百萬分之一小幾多

然而，你打車、坐地鐵、炒菜、逛街一輩子，能賺 2500 萬嗎？

2500 萬什么概念？

500 萬的存條目，理財適當就可以衣食無憂（每月躺著拿 1 萬元的投資收益）

2500 萬的存條目，光理財收益就可以吊打一線城市 95%以上的工薪階級

2500 萬存銀行，4%收益率，一年是 100 萬，存 3 年就可以在二線城市中間地段全條目買房，若是拿來還房貸，可以支撐 1400 萬的房貸，買 2000 萬的房子。

上海平均月工資 8000 多，2500 萬需要不吃不喝地攢 260 年。

而你需要承擔的，只不外是打車 200 次出事兒的風險

一些答本家兒口口聲聲說，幾多錢我都不會拿我的生命惡作劇，拒絕了 2500 萬的誘惑

一邊天天為了賺幾千幾萬塊錢，承受著更高的風險去打車趕公交趕高鐵……

若是這么一對比，你還會去做嗎？

歸正我就想問——這種游戲在哪兒做？？

我能玩到你破產

===============更了個新===========

評論區良多伴侶仍是不太可以或許區分“前提概率”和“自力事務概率”的不同

和大師會商會商挺有意思的，概率學我也沒怎么當真學過，友善切磋互惠互利

在這里稍微做一下科普吧，究竟結果高中數學隔太久大師忘失落了也正常

港真，這玩意兒很抽象，且有的時辰反直覺

搞混是常事

但非有一上來殉國正言辭說我錯了鄙夷我的……昂……年老你這又是何須……

Overconfidence 也是金融學的大忌好么……

就拿高峻上的伯努利試驗（其實就是扔鋼镚兒看正背面，伯努利這哥們兒叫的早，所以以他定名，占了個年數大的廉價）來舉例吧。

伯努利年老扔了 N 多次硬幣后，得出的結論是——不管之前扔了幾多次，下一次的概率依然是正面 50%，背面 50%，哪怕前面扔的 1000 次，都是古跡般地正面朝上，第 1001 次扔硬幣，呈現背面的概率仍然是 50%。

簡單的說，第一次和之后 1 萬次、一億次的扔硬幣成果都是互不影響的，每一次扔硬幣硬它都有本身的設法，大師是彼此自力的，這是自力事務概率

但我們此刻所要求的，不是自力事務的概率，而是由自力事務構成的持續事務中某個特心猿意馬組合發生的概率

這完全就是兩回事

這里我們用經典的二叉示范型做一次推導，為了簡練，我們只看持續扔三次，可能呈現幾多種環境（現實上是因為我懶）

第一次扔，有（正）（反）兩種可能，各 50%

第二次扔，有（正，正）（正，反）（反，正）（反，反）4 種可能，這個時辰持續兩次為正的概率就只有 4 種中的 1 種，即 25%

第三次扔，已經有了 2 的 3 次方也就是 8 種，別離為（正，正，正）（正，正，反）（正，反，正）（正，反，反）（反，正，正）（反，正，反）（反，反，正）（反，反，反），可以看到，持續三次為正的環境，在 8 種中只有 1 種，可能性是 1/8=12.5%

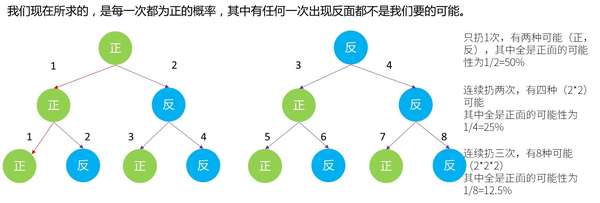
若是恰是生，反是死，那不管是 3 小我同時扔色子都在世，仍是 1 小我扔了三次之后還在世的概率，都是 12.5%

所以自力事務發生的概率不受之前發生的工作成果影響

但當所求的事務概率為一系列自力事務組成的整體事務中，某一前提發生的概率時，就需要疊加前面事務的概率，因為這是這個游戲仍然能繼續進行的前提

好比本問題中，要賺 2.5 個億，那就是持續 5000 次都生還的概率的乘積，中心任何一次，呈現了沒有生還的事務，城市讓游戲者就地歸天。那可能性就只有一種，就是 5000 次都生還，只有第一次，第二次都生還了，才有后續的可能。所以，持續保存 5000 輪，和持續保存 2 輪，存活率天然是紛歧樣的。

有的答本家兒很是機智，說，那我玩完 100 次之后，我決議不干，騙一下概率

然后我俄然！決議再玩！概率不就重置變回百萬分之一了嗎？？

棍騙一時爽，一向棍騙一向爽

可是……你之前玩的那 100 次，固然都活了下來，但每次都堆集了掛失落的概率啊……你之所以玩了 100 次還能棍騙概率，棍騙硬幣和伯努利，是因為你命運好玩了 100 次都沒掛啊，風險并不會因為沒有發生就消弭，也不會因為發生了之后就一路坦途，固然可能有點反常識，但想要棍騙概率，生怕不可。

發表于 2019-04-03 22:13
閱讀 ( 809 )
分類：其他類型

可以無償獲得 5000 元，但有 1/100 萬的幾率當場斃命，你會玩多少次這樣的游戲？

你可能感興趣的文章

相關問題

0 條評論

作家榜 ?

推薦文章