從水龍頭下落的水為何會越來越細？

圖片：kaboompics / CC0

姜小白71，力學

這個問題是射流現象(Fluid Jet or Jet)中最簡單的一個問題，一般稱為Free-Falling Fluid Jet問題。即便如斯，因為流體力學的復雜性，至今仍有學者在孜孜不倦地研究著這個問題。

當然，若是只是為領會釋糊口中的常見環境，那么現有研究成果仍是足夠的。我們起首心猿意馬性地看一下這個問題，從水龍頭中流出的水在重力的感化下不竭加快，是以流速是越來越大。而又因為流量守恒，截面積只會越來越小（流量=截面積 x 流速），是以水柱越來越細。接下來我們來心猿意馬量計較一下，這時辰就需要相關的流體力學常識了。

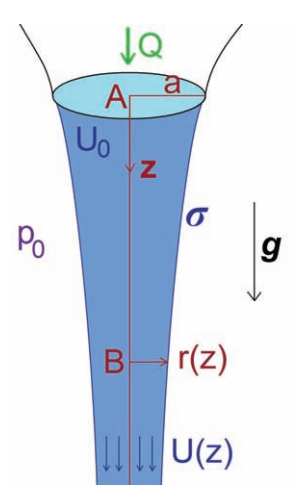
如上圖所示，我們考慮的流動是大雷諾數流動，此時流動可視為無粘流動(現實上水的粘性自己就很小)，但同時需要包管流動仍是層流。那么此刻流動可看作簡單的一維流動，我們可以在

$A,B$

兩點之間利用伯努利方程。

$\frac{1}{2}\rho U_0^2+\rho g z+P_A=\frac{1}{2}\rho U^2(z)+P_B$

考慮流量守恒則有

$Q=2\pi\int_0^r U(z)r(z)dr=\pi a^2U_0=\pi a^2U(z)$

考慮下面兩種環境，

（1）忽略概況張力。

此時

$P_A=P_B=P_0$

,按照上面兩式，可解得，

$\frac{r}{a}=\left(1+\frac{2gz}{U_0^2}\right)^{-1/4}$

$\frac{U(z)}{U_0}=\left(1+\frac{2gz}{U_0^2}\right)^{1/2}$

這就是水流半徑和流速隨高度的轉變關系式。當然，我們完全可以將水流理解為自由落體活動的，只是為了形式的同一性，才用伯努利方程暗示。下面跟嘗試成果對比一下。

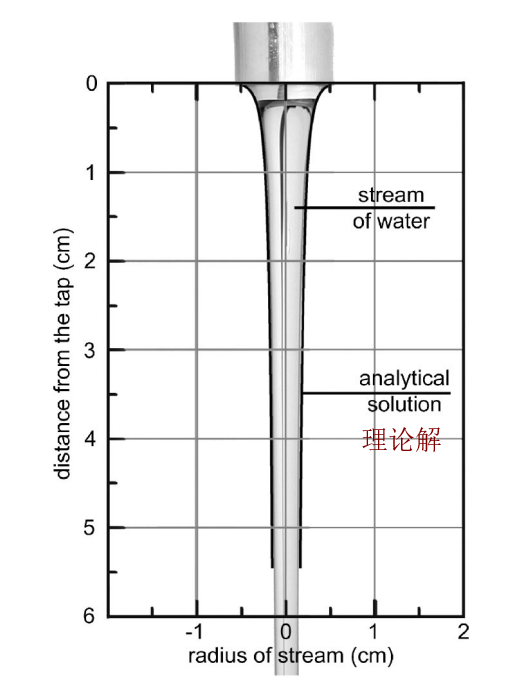
可以看到，上述理論成果與嘗試成果合適杰出。若是要詮釋糊口的現象，上面的公式就足夠了。為了知足大師的進修熱情，下面我們起頭進一步的闡發，這就是第二種環境。

（2）考慮概況張力。

按照 Young-Laplace 公式（不領會的話可拜見我的其他回覆），

$P_A\approx P_0+\frac{\sigma}{a}$

$P_B\approx P_0+\frac{\sigma}{r}$

按照伯努利方程和流量守恒，解得

$\frac{r(z)}{a}=\left(\frac{U0}{U(z)}\right)^{1/2}=\left[ 1+\frac{2}{Fr}\frac{z}{a}+\frac{2}{We}\left(1-\frac{a}{r} \right)\right]^{-1/4}$

式中，

$Fr=\frac{U_0^2}{ga}$

稱為 Fr 數（Froude Number）,表征慣性力和重力的相對巨細。

$We=\frac{\rho U_0^2a}{\sigma}$

稱為 We 數（Weber Number）,表征慣性力和概況張力的相對巨細。

這個公式插手了概況張力批改，是以合用規模更廣。而在日常糊口中的水龍頭流水現象中，We 數一般比力大，是以公式中的最后一項可以忽略失落，又回到了第一種環境，這意味著我們忽略概況張力是合理的。但要明白的是，我們是在無粘前提下進行會商的，若是考慮粘性的話，環境就更復雜了，良多文獻提出了各類粘性耗散的估量方式，有感樂趣的讀者可進一步參閱文末參考文獻。我注重到有良多人提到如下圖所示的水柱被拉斷并形當作液滴的環境，這其實是因為Plateau-Rayleigh 不不變性(The Plateau-Rayleigh Instability)，有機遇再答吧。

【參考文獻】

【1】Massalha, T., & Digilov, R. M. (2013). The shape function of a free-falling laminar jet: Making use of Bernoulli's equation.American Journal of Physics,81(10), 733-737.

【2】Grubelnik, V., & Marhl, M. (2005). Drop formation in a falling stream of liquid.American journal of physics,73(5), 415-419.

【3】Gamez-Montero, P. J., Castilla, R., Freire, J., Khamashta, M., & Codina, E. (2016). An empirical methodology for prediction of shape and flow rate of a free-falling non-submerged liquid and casting iron stream.Advances in Mechanical Engineering,8(9), 1687814016669635.

發表于 2019-04-11 22:55
閱讀 ( 1126 )
分類：其他類型

從水龍頭下落的水為何會越來越細？

你可能感興趣的文章

相關問題

0 條評論

作家榜 ?

推薦文章