常用的三角函數公式集合三角函數公式整理

常見的三角函數包括正弦函數、余弦函數和正切函數。在航海學、測繪學、工程學等其他學科中，還會用到如余切函數、正割函數、余割函數、正矢函數、余矢函數、半正矢函數、半余矢函數等其他的三角函數。三角函數（trigonometric function）是基本初等函數之一，是以角度（數學上最常用弧度制，下同）為自變量，角度對應任意角終邊與單位圓交點坐標或其比值為因變量的函數。下面是我們學習中常用的三角函數公式整理，請看下面。

操作方式

01
兩角和公式
兩角和（差）公式包羅兩角和差的正弦公式、兩角和差的余弦公式、兩角和差的正切公式。兩角和與差的公式是三角函數恒等變換的根本，其他三角函數公式都是在此公式根本上變形獲得的。
02
倍角公式
倍角公式，是三角函數中很是適用的一類公式。就是把二倍角的三角函數用本角的三角函數暗示出來。在計較中可以用來化簡計較式、削減求三角函數的次數，在工程中也有普遍的運用。
03
三倍角公式
三倍角公式是把形如sin(3x)、 cos(3x)等三角函數用對應單倍角三角函數暗示的恒等式。
04
半角公式
半角公式（Half angle formula）是操縱某個角（如∠A）的正弦值、余弦值、正切值，及其他三角函數值，來求其半角的正弦值，余弦值，正切值，及其他三角函數值的公式。
05
和差化積
和差化積是一種計較三角函數時所利用的數學公式。和差化積公式包羅正弦、余弦、正切和余切的和差化積公式，是三角函數中的一組恒等式，和差化積公式共10組。
06
誘導公式
誘導公式是指三角函數中，操縱周期性將角度比力大的三角函數，轉換為角度比力小的三角函數的公式。誘導公式有六組，共54個。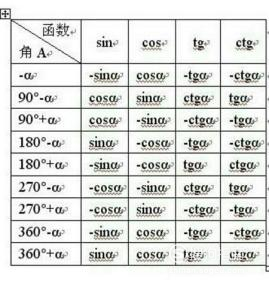
07
全能公式
全能公式包羅三角函數、導函數等。全能公式，可以把所有三角函數都化當作只有tan(a/2)的多項式之類的。將sinα、cosα、tanα代換當作tan(α/2)的式子，這種代換稱為全能置換的代換公式。
08
三角公式
三角公式，別名三角函數誘導公式，是三角函數之間的變換獲得的公式。三角公式具體有兩角和公式、倍角公式、和差化積公式、積化和差公式等。
09
其他非重點三角函數
csc(a) = 1/sin(a)

sec(a) = 1/cos(a)
10
雙曲函數
在數學中，雙曲函數是一類與常見的三角函數（也叫圓函數）近似的函數。最根基的雙曲函數是雙曲正弦函數sinh和雙曲余弦函數cosh，從它們可以導出雙曲正切函數tanh等，其推導也近似于三角函數的推導。雙曲函數的反函數稱為反雙曲函數。
11
降冪公式
sin2α=[1-cos（2α）]/2

cos2α=[1+cos（2α）]/2

tan2α=[1-cos（2α）]/[1+cos（2α）]
12
冪級數
它們的各項都是正整數冪的冪函數, 此中c0,c1,c2,...cn...及a都是常數，這種級數稱為冪級數。
End