優博地址

 知乎用戶,以誠為本,以樸修身,以勇求進,以毅立功
知乎用戶,以誠為本,以樸修身,以勇求進,以毅立功
進修數學范疇的一門科目標根本常識,無外乎兩個目標,一個是在測驗中取得好成就,一個是在理解這些常識中,能在本身的研究頂用到它。前一個目標良多回覆已經歸納綜合的很好,這里不再贅述,所以呢,就連系本身從上課到學做研究的一些體味來辦事于第二個目標讀者。
一門學科入門,有兩種方式,一種是從抽象到具體,一種是從具體到抽象。一起頭就是一個很嚴密的抽象的界說,以及隨之而來的一系列公式,對新手其實并不是很友愛,并且也并不克不及幫忙初學者細心的思慮這些公式和界說所蘊含的人類聰明。所以,我們就先從一些具體的案例出發,看看為啥線性代數里有那么多如“線性相關”似乎很無聊的概念以及環繞這些概念而來的理論吧。我們考慮三個比力根本的案例:線性方程組的求解;線段扭轉與線性變換;以及高維數據降維與聚類。前兩個是很經典的問題,最后一個是跟著統計學出格是大數據時代到來變得在分歧學科遍及呈現的問題。讓我們起頭吧。
1.案例 1:線性方程組的求解
從小學起頭,我們就起頭進修若何求解下面的方程組(這個方程組里,
是未知數,其他為已知數,m 紛歧心猿意馬等于 n):
方程組(1)簡練而又主要,因為很多理論以及簡單的模子最后都可以歸結為方程組(1)的求解。小學和初中進修的是加減消元法,高中后,算立體幾何題,求法標的目的量的時辰,會用到行列式來求解這個方程組。上大學前,我們對于線性代數最根基的問題,線性方程組的求解,并不是很目生。
不外,在讀者眉飛色舞的吭哧吭哧的求解方程組(1)的時辰,或許想過,以及在具體的算例中碰著過如下問題:
- 方程組(1)與方程
- 若何對行列式做到 n 個變量的推廣呢?與此相伴的問題時,行列式的事實該若何界說呢?
- 方程組(1)什么時辰有解,什么時辰沒有解,什么時辰詮釋獨一的,什么時辰解是不惟一的呢?
這三個問題,恰是一本尺度的線性代數教材里的前幾章的常識所致力于回覆的問題。解決思緒就是引入標的目的量空間,以及矩陣,那么(1)式可以形式上的寫作:
我們只要研究系數矩陣
以及增廣矩陣
就好了。怎么研究呢,那些絮絮不休的線性相關的理論就是為此辦事的。
若是我們考慮我們熟悉的實數域的環境,當系數矩陣是方陣時,我們將行列式視作空間
到數域
的映射,即:
若是我們按照一階行列式,二階行列式的公式,遞歸的界說行列式
可以證實(3)是獨一知足如下前提的映射:
1)將單元矩陣
映射為 1
2)
此中省略號的行標的目的量都是一樣的;
3) 若是矩陣
相鄰的行標的目的量不異,那么
用行列式,線性相關,基,秩這些概念,我們便可以成立起關于方程
的有解的判別前提,以及解的布局的心猿意馬理 ,這些尺度的教材里都有,就不再贅述了。值得注重的是,若是我們將這套理論,移植到可微函數構成的線性微分方程組,我們也可以機關近似的命題,這申明我們可以將 矩陣和標的目的量做更為一般的推廣。
2. 案例 2,線段扭轉與線性變換
若是讀者用過 PS 或者 PPT 的時辰,會發現里面的那些外形其實都是用坐標描述的,于是我們便可以將其視作
的一個子空間。考慮一個簡單的問題,我們需要對 PS 里位于坐標原點的一段線段逆時針扭轉必然的角度,PS 是若何實現這個功能的呢?很簡單,我們只需要對這段線段對應的標的目的量進行坐標變換就好了。若是進行變換呢?若是我們將方程(2)視作將標的目的量 x 變換為標的目的量 b,那么我們可以把矩陣 A“視作”一個變換。那么我們只要用一個二階矩陣來暗示扭轉變換就好了,這個二階矩陣,可所以
扭轉變換是更為稱為線性變換的具體案例,并且不改變線段的長度(連結距離)。此外,我們可以想象,若是一個標的目的量的偏向與扭轉的偏向一致,那么扭轉變換是不會改變其偏向的(這個標的目的量就是所謂特征標的目的量)。
尺度的線性代數教材的后半部門,很大水平上是對這個線段扭轉問題的擴展。矩陣的特征值,對角化,以及二次型的理論就是上面這個線段扭轉問題的進一步研究。此外,二次型的相關理論還可以幫忙我們回覆二次曲線和曲面分類的問題。具體可見任何一本尺度的線性代數教材,例如丘維聲的書,這里不再贅述。
3. 案例 3:高維數據降維與聚類
這個案例和筆者的專業很是相關了。素質上來說是數理統計與線性代數的交叉。
當前生物研究中有一個很是前沿的手藝,叫做單細胞轉錄組測序。例如我們可以從人身上抽外周血,進行單細胞測序,這些測序數據在顛末一系列的處置之后,最終會獲得一個稱之為表達矩陣的對象,此中每一行對應一個基因,每一列對應一個細胞,所以這個數據真的是一個矩陣。若是讀者看過《工作細胞》的話,或許知道外周血里有很多分歧類型的細胞,好比 T 細胞,B 細胞,這些細胞之所所以分歧的,真的是因為他們形態和功能特異。那么我們會問,可否從這么多細胞的表達譜將分歧的細胞類型找出來呢。當然是可以的。
假如我們測了 2700 個單細胞,人的參考基因組注釋出了 30000 個基因的話,那么我們的表達矩陣應該是
的十分稀少的矩陣。我們但愿能在二維的坐標圖中,盡可能的展示出細胞類型的信息,而且能區分出分歧的細胞類型。轉化為兩個子問題,那就是,高維矩陣降維,以及高維數據聚類的問題 。這中心有很多巧妙的算法。在實踐中,高維矩陣降維我們常用的是 PCA,t-SNE,UMAP 等算法,而聚類的話,我們會用條理聚類以及 Louvain Algorithm 之類的圖聚類算法,對每個細胞對應的高維標的目的量進行聚類;
我們可以看看具體的步調,這是 PCA 的成果,我們看到,細胞似乎能分為 4 個分歧的大類 ;
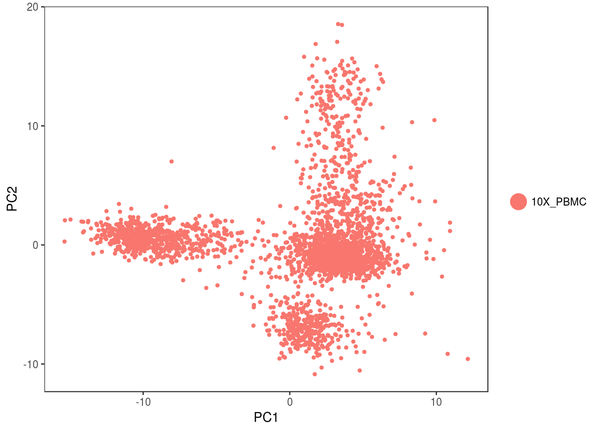
我們用非線性的降維方式 t-SNE,將這些細胞在二維的投影上分的更開,而且用 Louvain Algorithm,進行聚類 ,將聚類標簽,用分歧顏色展示出來;
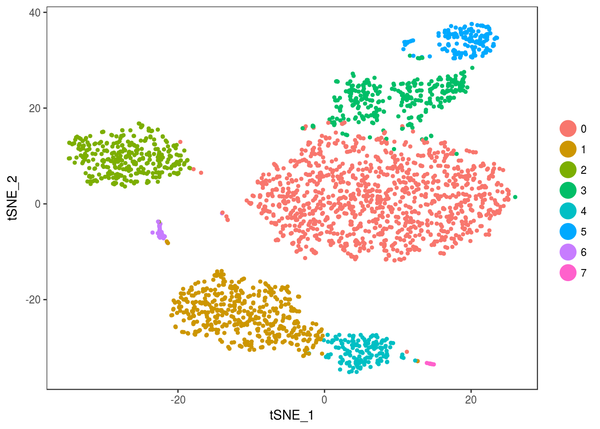
若是連系先驗常識,查看每個類別對應細胞的差別表達基因,我們可以對每個類別進行注釋,最終我們可以獲得下面的這個成果:
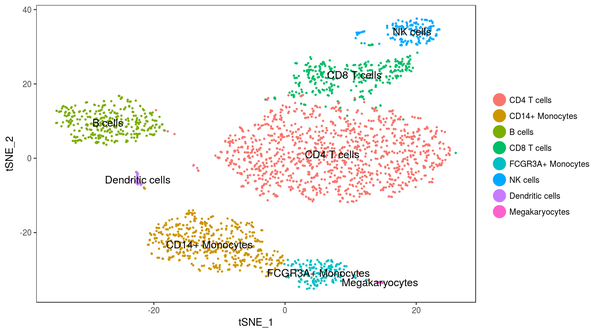
此外 ,還可以將 PCA 以及 t-SNE 納入到流形進修的框架里,有學者提出了 UMAP 算法 ,可以或許更好的可視化,降維與聚類成果。
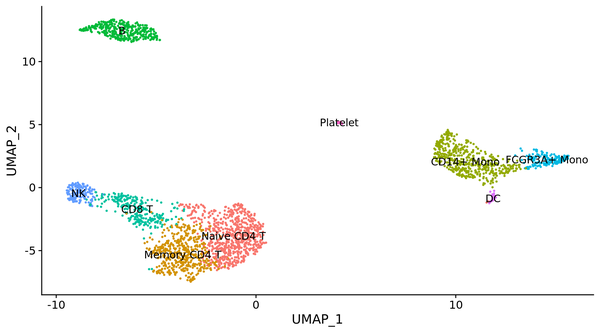
PCA,t-SNE,以及 UMAP 這些統計進修里的高級算法背后離不開矩陣闡發和泛函闡發(可以將其視為函數版本的線性代數)的相關理論,其策略就是界說懷抱空間以及范數,這里就不再做深切介紹了。只列出參考文獻:
PCA 的介紹可見李航的《統計進修方式》;
t-SNE 道理以及代碼實現見
UMAP 論文以及代碼實現見
- 發表于 2019-10-20 17:30
- 閱讀 ( 1723 )
- 分類:其他類型
你可能感興趣的文章
- 2019武漢軍運會怎么購買門票 861 瀏覽
- 如果把U盤插在充電器上會怎么樣 2314 瀏覽
- 不能初始化Photoshop,暫存盤已滿怎么辦 1077 瀏覽
- 淘寶開店店鋪簡介怎么寫 901 瀏覽
- 加泰羅尼亞為什么鬧獨立? 1037 瀏覽
- 一個社會主義者對蘇聯滅亡根源的解讀是什么? 936 瀏覽
- 人類是否真的是被困在地球上的囚徒?結果顛覆認知 929 瀏覽
- 高數學天賦的孩子應該獲得怎樣的教育? 1185 瀏覽
- 為什么司法使命在于“創新”或者“詮釋”? 970 瀏覽
- 都盯上了月球南極,那么南極到底發現了什么? 920 瀏覽
- 雙黃蛋會孵出什么樣的小雞? 1089 瀏覽
- 用數學來理解:人數的優勢究竟在戰爭中占據什么樣的地位? 971 瀏覽
- 骰寶游戲 863 瀏覽
- 經期心情煩躁怎么辦,6招緩解經期情緒急躁癥 1071 瀏覽
- 寶寶吃益生菌有哪些好處 742 瀏覽
- 如何選擇墨鏡 848 瀏覽
- 明仕 835 瀏覽
- 博貓彩票 876 瀏覽
- QQ空間農場中如何領取系統停機維護禮物 898 瀏覽
- 如何給圖片添加彩色鉛筆效果 925 瀏覽
- 上海一女漫畫家出租屋內意外離世,漫畫家的壓力究竟有多大? 842 瀏覽
- 瞎扯 · 如何正確地吐槽 876 瀏覽
- 汽車車身是越硬越安全嗎? 1448 瀏覽
- 利博 845 瀏覽
- 精子是怎么在茫茫子宮中找到小小卵子的? 1425 瀏覽
- 怎么管理能力比你強的下屬? 1327 瀏覽
- 網絡老虎機 1062 瀏覽
- 辭職報告范文怎么寫 764 瀏覽
- 小個子打籃球技巧 819 瀏覽
- 打好籃球要掌握哪些技巧 756 瀏覽
相關問題
0 條評論
0 篇文章
作家榜 ?
-
 xiaonan123
189 文章
xiaonan123
189 文章
-
 湯依妹兒
97 文章
湯依妹兒
97 文章
-
 luogf229
46 文章
luogf229
46 文章
-
 jy02406749
45 文章
jy02406749
45 文章
-
 小凡
34 文章
小凡
34 文章
-
 Daisy萌
32 文章
Daisy萌
32 文章
-
 我的QQ3117863681
24 文章
我的QQ3117863681
24 文章
-
 華志健
23 文章
華志健
23 文章
推薦文章
- 玫瑰花花苞還沒開就焦枯了是怎么回事
- 日本雅虎郵箱如何修改密碼
- matlab find用法
- Vue如何新建項目及Vue
- 視頻怎么換封面
- 七天娛樂
- 表格怎樣設置點到某單元格時所在行顏色有變化
- 水果競猜
- 怎么查詢對方qq的ip地址 如何通過qq查看對方ip
- win10和win7雙系統如何跳過開機自檢磁盤
- 企業郵箱怎么綁定qq郵箱
- 啟動CAD提示文件加載安全問題怎樣解決
- 怎么樣在公眾號植入直播
- 如何提高月季扦插生根后假植成活率
- 淘寶賣家怎么找貨源
- 盆栽朱頂紅什么時候換盆合適
- SQLyog如何創建觸發器,詳細教程
- SQLyog如何備份數據庫,詳細教程
- 山西娘子關游玩攻略
- 北京園博園一日游攻略
- 駕車遇險應該怎么急救
- 新不夜城論壇
- 可愛女寶形象設計
- 名人宣傳畫設計
- 拔河規則及技巧
- 如何使用健腹輪
- 口袋妖怪最強進化3.0普通版攻略
- 王者榮耀周瑜戰令限定皮膚赤蓮之焰怎么獲得
- 王者模擬戰精靈阿雞怎么獲得
- 王者榮耀蘭陵王戰令限定皮膚訓魔獵人怎么獲得