【MATLAB】常用的創建矩陣的方法
東西/原料
- 計較機
- MATLAB
方式/步調
- 1
號令行窗口直接輸入矩陣，這是最簡單的方式。
1.所有元素置于[ ]內；
2.每一行的各元素之間用逗號“,”或空格“ ”離隔，注重逗號為英文符號；
3.各行之間用分號“;”或回車離隔，注重分號為英文符號。
- 2
用冒號生當作矩陣，冒號“:”可以發生步長相等的行標的目的量。
- 3
用linspace函數建立矩陣。linspace函數挪用為：
x=linspace(a,b,n)
此中a為初值，b為終值，n為元素數目（n省略時發生100個元素）。
該函數生當作一個等差數列。
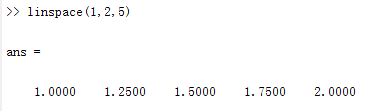
- 4
用logspace函數建立矩陣。logspace函數挪用為：
x=logspace(a,b,n)
第一個元素為10^a，最后一個元素為10^b，n為元素數目。
該函數生當作一個對數等比數列。
- 5
單元矩陣的建立。利用eye函數，挪用格局為：
A=eye(n) 生當作n×n階矩陣；
A=eye(m,n) 生當作m×n階矩陣；
A=eye(size(B)) 生當作與B矩陣巨細不異的單元矩陣。
- 6
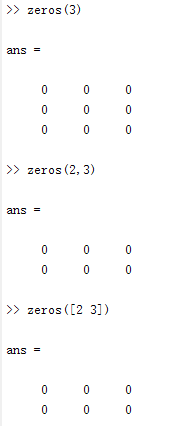
0矩陣的建立。利用zeros函數，挪用格局為：
A=zeros(n) 生當作n×n階0矩陣；
A=zeros(m,n) 生當作m×n階0矩陣；
A=zeros([m n]) 生當作m×n階0矩陣；
A=zeros(size(B)) 生當作與B矩陣巨細不異的0矩陣。
- 7
1矩陣的建立。利用ones函數，挪用格局為：
A=ones(n) 生當作n×n階1矩陣；
A=ones(m,n) 生當作m×n階1矩陣；
A=ones([m n]) 生當作m×n階1矩陣；
A=ones(size(B)) 生當作與B矩陣巨細不異的1矩陣。
- 8
魔方矩陣的建立。魔方矩陣指各行各列和對角線元素和相等的矩陣，利用magic函數，挪用格局為：
A=magic(n)
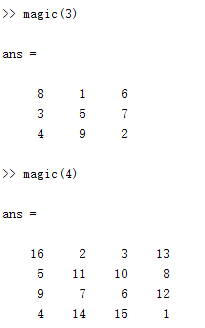
- 9
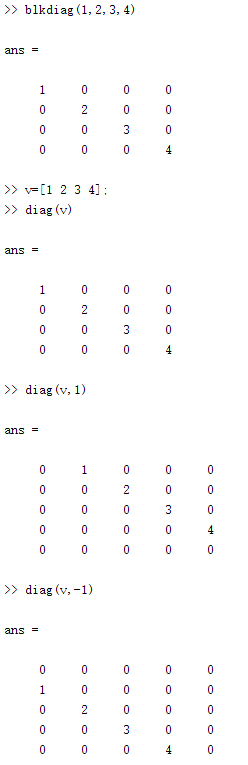
發生以輸入元素為對角元素的矩陣。格局為：
A=blkdiag(a,b,c,...)；
A=diag(v,k) 以v的元素為A矩陣第k條對角線的元素。
- 10
三角矩陣的建立。挪用函數為：
A1=tril(A,k) 生當作A矩陣中第k條對角線的下三角部門矩陣；
A2=triu(A,k) 生當作A矩陣中第k條對角線的上三角部門矩陣。
END
注重事項
- 注重“,”、“:”、“;”等符號均為英文符號。
- 矩陣建立為MATLAB的根基功，應多加操練，熟能生巧。
- 發表于 2020-06-07 17:40
- 閱讀 ( 1209 )
- 分類：其他類型
0 篇文章
作家榜 ?
-
xiaonan123
189 文章
-
湯依妹兒
97 文章
-
luogf229
46 文章
-
jy02406749
45 文章
-
小凡
34 文章
-
Daisy萌
32 文章
-
我的QQ3117863681
24 文章
-
華志健
23 文章